Bạn đang xem bài viết Công thức tính diện tích hình thoi? Giải bài tập lớp 4 và lớp 8 tại Mas.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Công thức tính diện tích hình thoi là một trong những khái niệm cơ bản về hình học mà chúng ta học từ lớp 4 và tiếp tục áp dụng trong lớp 8. Việc hiểu và áp dụng công thức này sẽ giúp chúng ta tính toán diện tích của một hình thoi một cách dễ dàng và chính xác.
Để tính diện tích hình thoi, chúng ta cần biết hai thông tin cơ bản là độ dài đường chéo dài và độ dài đường chéo ngắn của hình. Sau đó, ta áp dụng công thức sau:
Diện tích hình thoi = Đường chéo dài x Đường chéo ngắn / 2
Ở lớp 4, chúng ta thường gặp các bài tập đơn giản liên quan đến tính diện tích hình thoi. Ví dụ, cho bài toán: “Hình thoi ABCD có đường chéo dài 8 cm và đường chéo ngắn 6 cm. Tính diện tích hình thoi ABCD.” Ta áp dụng công thức trên, ta có: Diện tích hình thoi ABCD = 8 cm x 6 cm / 2 = 24 cm2.
Tuy nhiên, khi chúng ta lên lớp 8, bài tập về diện tích hình thoi sẽ phức tạp hơn. Chúng ta sẽ phải áp dụng kiến thức về hình học và giải tích để giải quyết các bài toán phức tạp hơn. Ví dụ, “Hình thoi ABCD có biết đường chéo dài 10 cm và diện tích hình thoi là 36 cm2. Tính độ dài đường chéo ngắn của hình thoi ABCD.” Để giải bài toán này, chúng ta phải đưa ra phương trình và áp dụng công thức tính diện tích hình thoi. Sau đó, giải phương trình để tìm ra độ dài đường chéo ngắn.
Tóm lại, công thức tính diện tích hình thoi là một kiến thức căn bản trong hình học mà chúng ta học từ lớp 4 và áp dụng tiếp trong lớp 8. Hiểu và áp dụng công thức này sẽ giúp chúng ta giải quyết các bài tập liên quan đến diện tích hình thoi một cách dễ dàng và chính xác.
Bạn có đang thắc mắc rằng có bao nhiêu công thức tính diện tích hình thoi? Hãy cùng Mas.edu.vn giải đáp những câu hỏi của bạn liên quan đến kiến thức về hình thoi nhé!
Danh Mục Bài Viết
Hình thoi là gì?
Định nghĩa hình thoi
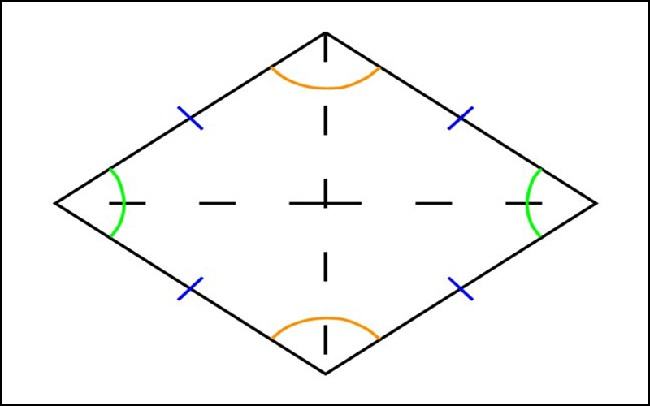
Hình thoi là hình tứ giác có bốn cạnh bằng nhau.
Hình thoi cũng chính là hình bình hành có hai cặp cạnh kề bằng nhau hoặc hai đường chéo vuông góc với nhau. Từ đó, hình thoi là hình có đầy đủ các tính chất của hình bình hành.
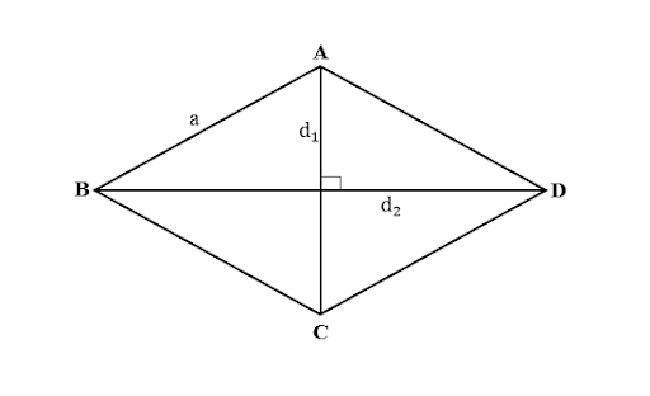
Tính chất hình thoi
Ngoài những tính chất giống với hình bình hành. Tính chất hình thoi được thể hiện như sau:
- Hình thoi có hai đường chéo vuông góc với nhau.
- Hình thoi có hai đường chéo chính là đường phân giác của các góc trong hình thoi.
- Hình thoi là hình có các góc đối bằng nhau. Tổng các góc trong hình thoi bằng 360 độ.
- Hình thoi có hai đường chéo vuông góc và cắt nhau tại trung điểm của mỗi đường.
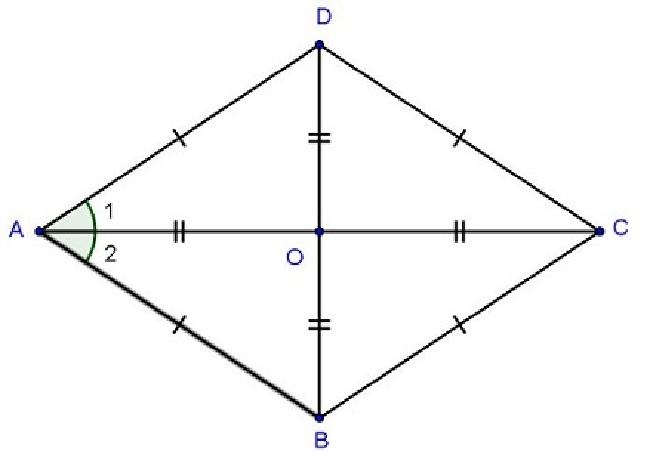
Dấu hiệu nhận biết hình thoi
Hình thoi có các dấu hiệu nhận biết như sau:
- Hình tứ giác mà có bốn cạnh bằng nhau là hình thoi.
- Hình bình hành mà có hai cạnh kề bằng nhau là hình thoi.
- Hình bình hành mà có hai đường chéo vuông góc với nhau là hình thoi.
- Hình bình hành mà có đường chéo là đường phân giác của một góc là hình thoi.
Sau khi đã tìm hiểu về rõ về định nghĩa, tính chất và dấu hiệu nhận biết hình thoi thì hãy cùng Mas.edu.vn đi vào phần chính trong nội dung công thức tính diện tích hình thoi bạn nhé!
Công thức tính diện tích hình thoi
Công thức tính diện tích hình thoi dựa theo đường chéo
Đường chéo của hình thoi là đường nối các đỉnh đối diện với nhau trong hình thoi.
Trong công thức tính diện tích hình thoi dựa vào đường chéo, bạn có thể làm theo 3 bước sau:
- Bước 1: Xác định được độ dài hai đường chéo.
- Bước 2: Nhân độ dài hai đường chéo lại với nhau.
- Bước 3: Lấy kết quả vừa tìm được chia cho 2.
Giả sử chúng ta có hình thoi ABCD có đường chéo AC và BD thì công thức tính diện tích hình thoi dựa theo đường chéo sẽ là: 1/2 x AC x BD.
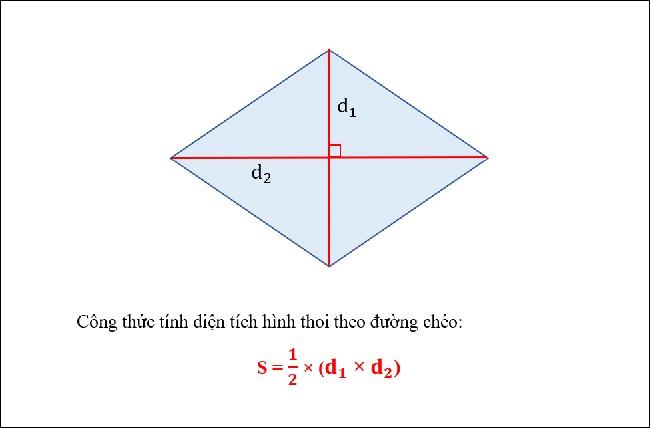
Ví dụ: Hình thoi ABCD có độ dài hai đường chéo AC và BD lần lượt là 5cm và 4cm. Hãy tính diện tích hình thoi?
Trả lời: Dựa vào công thức tính diện tích hình thoi dựa theo đường chéo ta có:
Diện tích hình thoi ABCD là:
(5 x 4) : 2= 10cm2
Công thức tính diện tích hình thoi dựa vào cạnh đáy và chiều cao
Bạn cũng có thể sử dụng công thức tính diện tích hình thoi dựa vào cạnh đáy và chiều cao. Chúng ta thể làm theo 2 bước sau:
- Bước 1: Xác định được độ dài đáy và chiều cao.
- Bước 2: Nhân độ dài đáy và chiều cao lại với nhau.
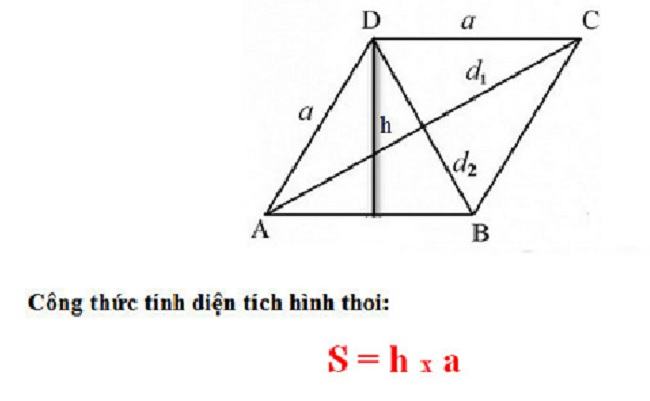
Ví dụ: Hình thoi ABCD có độ dài cạnh đáy là 10cm và có chiều cao là 8cm. Tính diện tích hình thoi?
Trả lời: Dựa vào công thức tính diện tích hình thoi dựa vào cạnh đáy và chiều cao ta có:
Diện tích hình thoi ABCD là:
10 x 8= 80cm2
Công thức tính diện tích hình thoi dựa vào hệ thức lượng trong tam giác
Nếu biết được số đo góc của hình thoi. Bạn cũng có thể sử dụng công thức tính diện tích hình thoi dựa vào hệ thức lượng trong tam giác.
Bạn có thể làm theo các bước sau:
- Bước 1: Vì hình thoi là hình có 4 cạnh bằng nhau. Nên bạn hãy xác định một độ dài cạnh bất kì.
- Bước 2: Bình phương chiều dài cạnh vừa xác định được.
- Bước 3: Nhân kết quả vừa tìm được với sin của một trong các góc bất kì của hình thoi.
Giả sử trong một hình thoi ABCD có cạnh a và các góc A,B,C,D thì bạn có thể tính diện tích hình thoi như sau:
S = a2.sinA = a2.sinB = a2.sinC = a2.sinD (trong đó a2 là bình phương cạnh a)
Ví dụ: Hình thoi ABCD có độ dài cạnh bằng 4cm và góc A bằng 33 độ. Hãy tính diện tích hình thoi ABCD?
Trả lời: Dựa vào công thức tính diện tích hình thoi dựa vào hệ thức lượng trong tam giác ta có:
Diện tích hình thoi ABCD là:
4^2 x sin(33)= 16 x 1= 16cm2.
Xem thêm:
- Công thức muốn tính diện tích hình vuông – Lớp 3, 4, 5
- Công thức tính cạnh huyền tam giác vuông đầy đủ nhất
- Công thức tính nửa chu vi hình chữ nhật – Lớp 3, Lớp 4
Lưu ý khi tính diện tích hình thoi
Khi tính diện tích hình thoi, bạn cần phải lưu ý hai điều sau:
- Đơn vị khi tính diện tích hình thoi phải cm2, m2, dm2,…
- Chú ý về đơn vị của độ dài hai đường chéo khi tính diện tích hình thoi dựa vào hai đường chéo. Hãy chắc chắn rằng độ dài của hai đường chéo đang cùng một đơn vị.
Bài tập liên quan đến tính diện tích hình thoi
Bài tập 1 trang 142 SGK Toán 4
Tính diện tích của:
a) Hình thoi ABCD, biết AC = 3cm, BD = 5cm
b) Hình thoi MNPQ, biết MP = 7cm, NQ = 4cm
Trả lời:
a) Hình thoi ABCD có hai đường chéo AC và BD. Dựa vào công thức tính diện tích hình thoi dựa theo hai đường chéo ta có:
Diện tích hình thoi ABCD là:
(3×5):2= 15/2 cm2
b) Hình thoi MNPQ có hai đường chéo là MP và NQ. Dựa vào công thức tính diện tích hình thoi dựa theo hai đường chéo ta có:
Diện tích hình thoi ABCD là:
(7×4):2= 14 cm2
Bài tập 2 trang 142 SGK Toán 4
Tính diện tích hình thoi biết:
a) Độ dài các đường chéo là 5dm và 20dm.
b) Độ dài các đường chéo là 4m và 15dm.
Trả lời:
a) Diện tích hình thoi là:
(5×20):2 = 50 dm2
b) Ta có 4m = 40dm
Diện tích hình thoi là:
(40×15):2= 300 dm2
Bài tập 3 trang 143 SGK Toán 4
Ghi Đúng (Đ) sai (S):
a) Diện tích hình thoi bằng diện tích hình chữ nhật
b) Diện tích hình thoi bằng 1/2 diện tích hình chữ nhật
Trả lời:
Diện tích hình thoi có độ dài hai đường chéo lần lượt là 5cm và 2cm là:
(5×2):2 = 5 cm2
Diện tích hình chữ nhật có chiều dài và chiều rộng lần lượt là 5cm và 2cm là:
5×2= 10 cm2
Vậy a là câu sai; b là câu đúng
Bài 33 trang 128 SGK Toán 8
Vẽ hình chữ nhật có một cạnh bằng đường chéo của một hình thoi cho trước và có diện tích bằng diện tích của hình thoi đó. Từ đó suy ra cách tính diện tích hình thoi.
Trả lời:
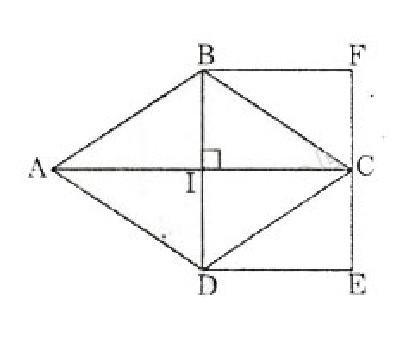
Cho hình thoi ABCD, vẽ hình chữ nhật có một cạnh là đường chéo BD, cạnh kia bằng IC (bằng nửa AC).
Khi đó diện tích của hình chữ nhật BDEF bằng diện tích hình thoi ABCD.
Ta có: S BDEF= BDxDE= BDxIC= BDxAC/2= (ACxBD):2
Vậy diện tích hình thoi bằng nửa tích hai đường chéo.
Bài 34 trang 128 SGK Toán 8
Cho một hình chữ nhật. Vẽ tứ giác có các đỉnh là trung điểm các cạnh của hình chữ nhật. Vì sao tứ giác này là một hình thoi? So sánh diện tích hình chữ nhật, từ đó suy ra cách tính diện tích hình thoi.
Trả lời:
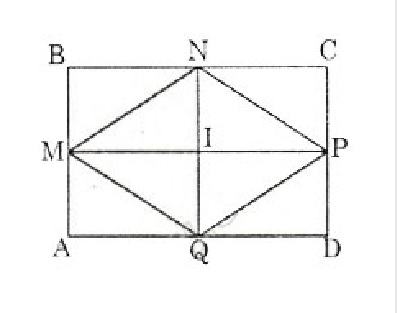
Vẽ hình chữ nhật ABCD với các trung điểm các cạnh là M, N, P, Q.
Vẽ tứ giác MNPQ
Ta có MN là đường trung bình của tam giác ABC nên MN= 1/2 AC
PQ là đường trung bình của tam giác ADC nên PQ= 1/2 AC
Vì vậy MN=PQ= 1/2AC (1)
Ta có MQ là đường trung bình của tam giác ABD nên MQ= 1/2 BD
NP là đường trung bình của tam giác BCD nên NP= 1/2 BD
Vì vậy MQ=NP= 1/2 BD (2)
Mà ABCD là hình chữ nhật nên AC=BD (3)
Từ (1), (2), (3) ta có MN = PQ = MQ = NP
=> Tứ giác MNPQ là hình thoi.
+ Ta có:
∆ BMN = ∆ IMN; ∆ INP = ∆ CNP, ∆ AMQ= ∆IMQ, ∆ DPQ= ∆IPQ
Vì vậy S MNPQ= 1/2 S ABCD
Mà S ABCD= ABxAD= MPxNQ
Vậy diện tích hình thoi bằng nửa tích hai đường chéo.
Bài 35 trang 129 SGK Toán 8
Tính diện tích hình thoi có cạnh dài 6cm và một trong các góc của nó có số đo là 60 độ.
Trả lời:
ΔABD là tam giác đều nên BD = AB = 6cm
I là giao điểm của AC và BD => AI ⊥ DB
⇒ AI là đường cao của tam giác đều ABD nên
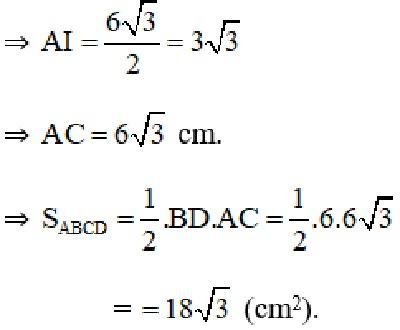
Bài 36 trang 129 SGK Toán 8
Cho một hình thoi và một hình vuông có cùng chu vi. Hỏi hình nào có diện tích lớn hơn? Vì sao?
Trả lời:
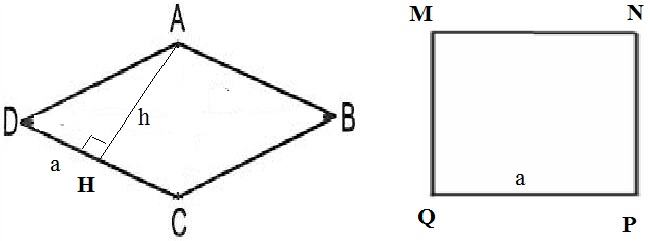
Giả sử cho hình thoi ABCD và hình vuông MNPQ có cùng chu vi là 4a
Vậy cạnh hình thoi và cạnh hình vuông đều có độ dài là a
Ta có: S MNPQ = a^2
Từ đỉnh góc A của hình thoi ABCD, ta vẽ đường cao AH có độ dài là h.
ABCD là hình thoi
⇒ ABCD là hình bình hành
⇒ S ABCD = ah
Mà ta có h ≤ a (đường vuông góc nhỏ hơn đường xiên)
⇒ ah ≤ a^2 ⇒ SABCD ≤ SMNPQ
Vậy diện tích hình vuông luôn lớn hơn diện tích hình thoi.
Trên đây là toàn bộ kiến thức liên quan đến công thức tính diện tích hình thoi. Hãy theo dõi Mas.edu.vn mỗi ngày để biết thêm nhiều thông hay và bổ ích nhé!
Trong bài viết này chúng ta đã tìm hiểu về công thức tính diện tích hình thoi và giải các bài tập lớp 4 và lớp 8 liên quan đến nó.
Đầu tiên, chúng ta đã nhắc lại rằng hình thoi là một hình bốn cạnh có cả bốn cạnh bằng nhau và hai đường chéo cắt nhau vuông góc. Để tính diện tích của một hình thoi, ta sử dụng công thức:
Diện tích hình thoi = độ dài cạnh x chiều cao
– Trong trường hợp của lớp 4, chúng ta đã thực hiện một số bài tập đơn giản như tính diện tích của một hình thoi khi biết cạnh và chiều cao. Đây là những bài tập giúp các em nắm vững công thức cơ bản và áp dụng nó vào các bài tập thực tế.
– Tiếp theo, trong bài viết này, chúng ta đã giải các bài tập lớp 8 liên quan đến hình thoi. Các bài tập này đòi hỏi khả năng áp dụng công thức tính diện tích trong các bài toán phức tạp hơn. Chúng ta đã tính diện tích của hình thoi khi biết cạnh, chiều cao, đường chéo và giá trị của góc. Chúng ta cũng đã giải quyết các bài toán tìm giá trị chưa biết, trong đó chúng ta được cho diện tích và một số thông số và ta phải tìm giá trị chưa biết.
Tóm lại, thông qua việc giải các bài tập về hình thoi, chúng ta đã áp dụng công thức tính diện tích trong các bài toán thực tế. Việc nắm vững công thức này cũng giúp chúng ta phát triển khả năng tính toán, logic và tư duy về số học. Hy vọng qua bài viết này, các em lớp 4 và lớp 8 đã hiểu và có thể áp dụng công thức tính diện tích hình thoi vào việc giải các bài tập.
Cảm ơn bạn đã xem bài viết Công thức tính diện tích hình thoi? Giải bài tập lớp 4 và lớp 8 tại Mas.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Diện tích hình thoi
2. Công thức tính diện tích hình thoi
3. Hình thoi
4. Tính diện tích
5. Công thức tính diện tích
6. Bài tập lớp 4 về hình thoi
7. Bài tập lớp 8 về hình thoi
8. Tính diện tích hình thoi bằng cạnh và đường cao
9. Tính diện tích hình thoi bằng đường chéo
10. Diện tích hình thoi là bán tính cạnh với đường chéo
11. Công thức diện tích hình thoi = cạnh x đường cao
12. Bài tập tính diện tích hình thoi lớp 4
13. Bài tập tính diện tích hình thoi lớp 8
14. Học cách tính diện tích hình thoi
15. Bài tập về công thức diện tích hình thoi.