Bạn đang xem bài viết Các trường hợp đồng dạng của tam giác vuông cần nhớ tại Mas.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Tam giác vuông là một trong những hình học cơ bản và quan trọng trong toán học và hình học. Điều đặc biệt là tam giác vuông có nhiều trường hợp đồng dạng khác nhau, mỗi trường hợp đều có những đặc điểm và quy tắc riêng. Đồng dạng trong hình học là khái niệm toán học chỉ sự tương tự về hình dạng, không xét đến kích thước của các hình. Việc hiểu và nhớ các trường hợp đồng dạng của tam giác vuông không chỉ giúp chúng ta phân biệt và phân loại các hình tam giác một cách chính xác mà còn giúp chúng ta giải quyết các bài toán liên quan đến tam giác vuông một cách dễ dàng và hiệu quả hơn. Bài viết này sẽ giới thiệu một số trường hợp đồng dạng của tam giác vuông cần nhớ và áp dụng trong thực tiễn.
Bài toán hình học về tam giác đồng dạng thường rất dễ gặp trong thi cử. Do đó bài viết sau sẽ mang đến cho bạn đọc những kiến thức về các trường hợp đồng dạng của tam giác vuông. Mời bạn đọc theo dõi cùng Mas.edu.vn.
Áp dụng các trường hợp đồng dạng của tam giác vuông
Hai tam giác vuông đồng dạng với nhau khi:
- Tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia.
- Tam giác vuông này có hai cạnh góc vuông tỉ lệ tương ứng với hai cạnh góc vuông của tam giác vuông kia.
Vừa rồi là lý thuyết các trường hợp đồng dạng của tam giác vuông. Để biết rõ hơn về dấu hiệu nhận biết các trường hợp đồng dạng của tam giác vuông, mời bạn đọc theo dõi nội dung sau.
Dấu hiệu nhận biết các trường hợp đồng dạng của tam giác vuông
Dưới đây là một số dấu hiệu nhận biết các trường hợp đồng dạng của tam giác vuông:
Định lý 1:
Hai tam giác vuông đồng dạng nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia.
Tổng quát: Δ ABC, Δ A’B’C’, góc A = góc A’ = 900; B’C’/BC = A’B’/AB
Suy ra: Δ ABC ~ Δ A’B’C’.
Kiến thức trên là dấu hiệu nhận biết các trường hợp đồng dạng của tam giác vuông. Tiếp nối bài viết là tỉ số hai đường cao, tỉ số diện tích của hai tam giác đồng dạng. Mời bạn đọc theo dõi cùng Mas.edu.vn.
Tỉ số hai đường cao, tỉ số diện tích của hai tam giác đồng dạng
Định lý 2:
Tỉ số hai đường cao tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.

Định lý 3:
Tỉ số diện tích hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.

Nội dung mở rộng:
Nếu hai tam giác đồng dạng với nhau thì ta có các tính chất sau:
- Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng.
- Tỉ số hai đường phân giác tương ứng bằng tỉ số đồng dạng.
- Tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng.
- Tỉ số các chu vi bằng tỉ số đồng dạng.
- Tỉ số các diện tích bằng bình phương tỉ số đồng dạng.
Toàn bộ thông tin trên là lý thuyết về các trường hợp đồng dạng của tam giác vuông. Để hiểu rõ hơn về kiến thức hình học thì nội dung dưới đây là một số bài tập áp dụng trong sách giáo khoa. Mời bạn đọc cùng tham khảo.
Xem thêm:
- Công thức tính cạnh huyền tam giác vuông đầy đủ nhất
- Các trường hợp bằng nhau của tam giác vuông Toán lớp 7
- Công thức tính đường cao trong tam giác đều dễ nhớ nhất
Bài tập về các trường hợp đồng dạng của tam giác vuông SGK Toán 8
Bài 8 trang 81 SGK Toán 8 tập 2
Câu hỏi: Hãy chỉ ra các cặp tam giác đồng dạng trong hình 47.
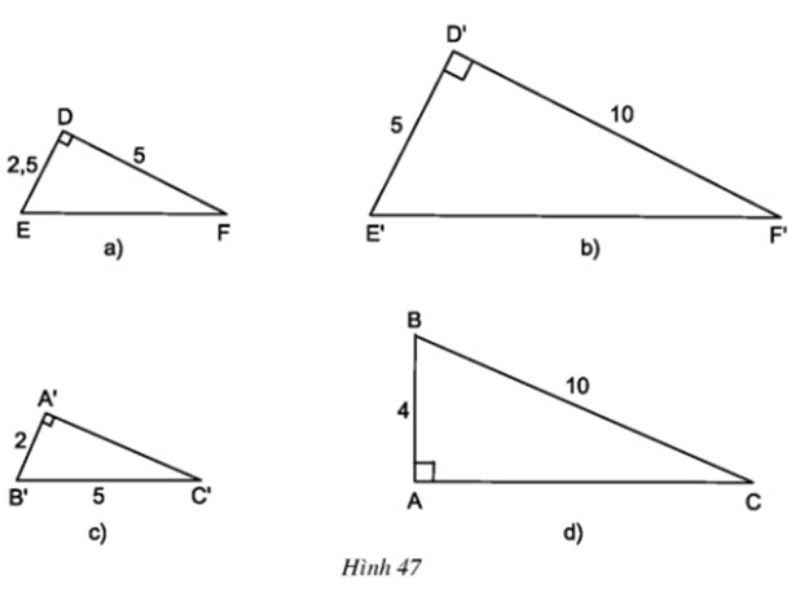
Trả lời:
ΔDEF vuông tại D và ΔD’E’F’ vuông tại D’ có:
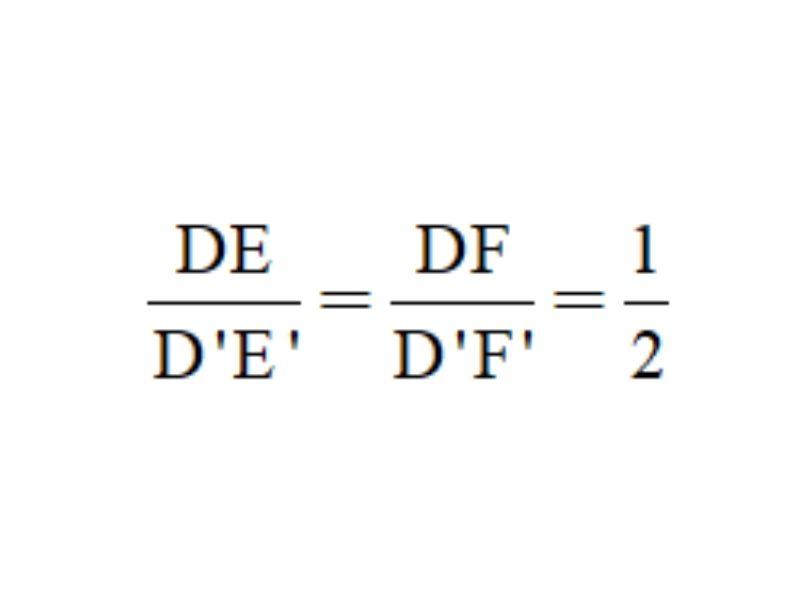
⇒ ΔDEF ∼ ΔD’E’F’ (hai cạnh góc vuông)
Áp dụng định lí Pytago vào tam giác A’B’C’ vuông tại A’ có:
A’C’2 + A’B’2 = B’C’2
=> A’C’2 + 22 = 52
Suy ra: A’C’2 = 25 – 4 = 21 nên A’C’ =
Áp dụng định lí Pytago vào tam giác ABC vuông tại A có:
AB2 + AC2 = BC2
Thay số: 42 + AC2 = 102
Suy ra: AC2 = 100 – 16 = 84 nên

Do đó, ∆ A’B’C’ đồng dạng với tam giác ABC (hai góc vuông tỉ lệ).
Bài 46 trang 84 SGK Toán 8 tập 2
Câu hỏi: Trên hình 50 hãy chỉ ra các tam giác đồng dạng. Viết các tam giác này theo thứ tự các đỉnh tương ứng và giải thích vì sao chúng đồng dạng?
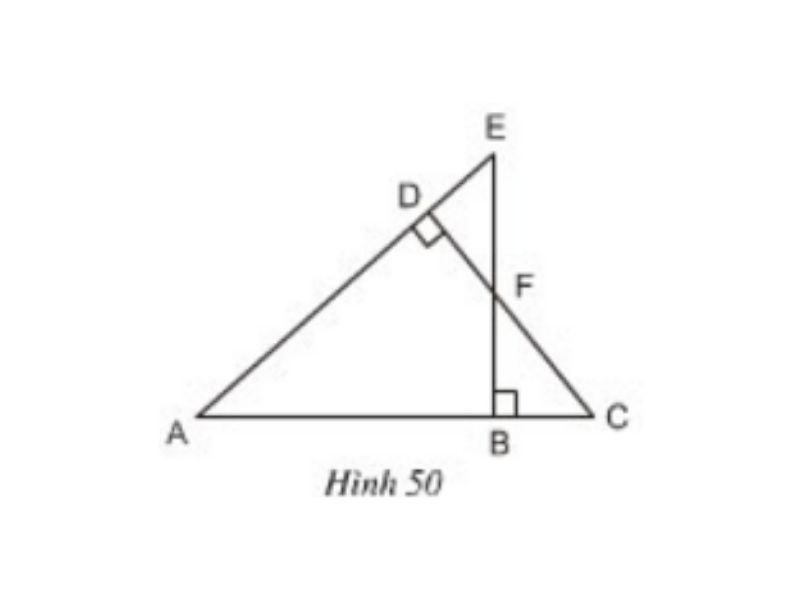
Trả lời:
Xét ∆DAC và ∆BAE ta có:
Góc A chung.
Góc D = góc B = 90o
=> ∆DAC ~ ∆BAE (g-g)
Xét ∆DFE và ∆BFC ta có:
Góc D = góc B = 90o
Góc DFE = góc BFC (đối đỉnh)
=> ∆DFE ~ ∆BFC (g-g)
Xét ∆DFE và ∆BAE ta có:
Góc D = góc B = 90o
Góc E chung
=> ∆DFE ~ ∆BAE (g-g)
Do đó: ∆DAC ~ ∆BAE ~ ∆DFE ~ ∆BFC
Bài 47 trang 84 SGK Toán 8 tập 2
Câu hỏi: Tam giác ABC có độ dài các cạnh là 3cm, 4cm, 5cm. Tam giác A’B’C’ đồng dạng với tam giác ABC và có diện tích là 54cm2. Tính độ dài các cạnh của tam giác A’B’C’.
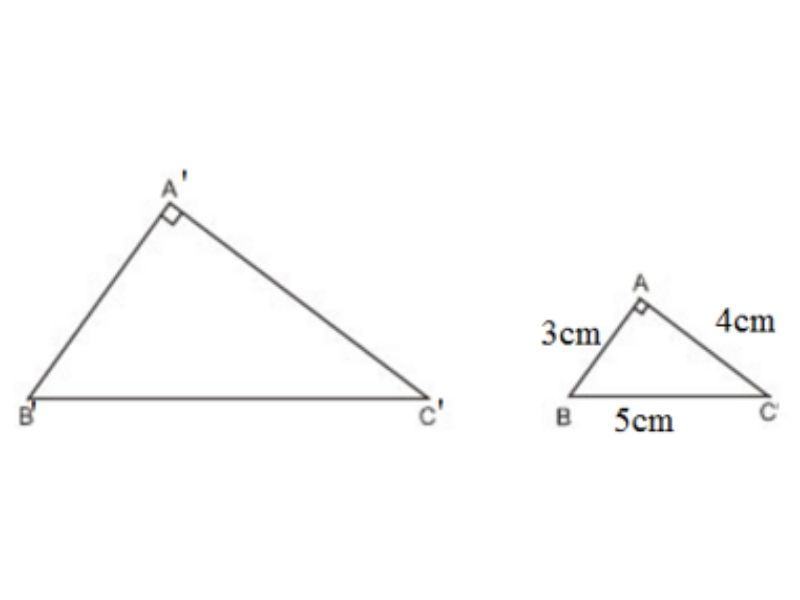
Trả lời:
Xét ΔABC có: AB2 + AC2 = 32 + 42 = 25 = 52 = BC2
⇒ ΔABC vuông tại A (Định lý Pytago đảo)
⇒ Diện tích tam giác ABC bằng:
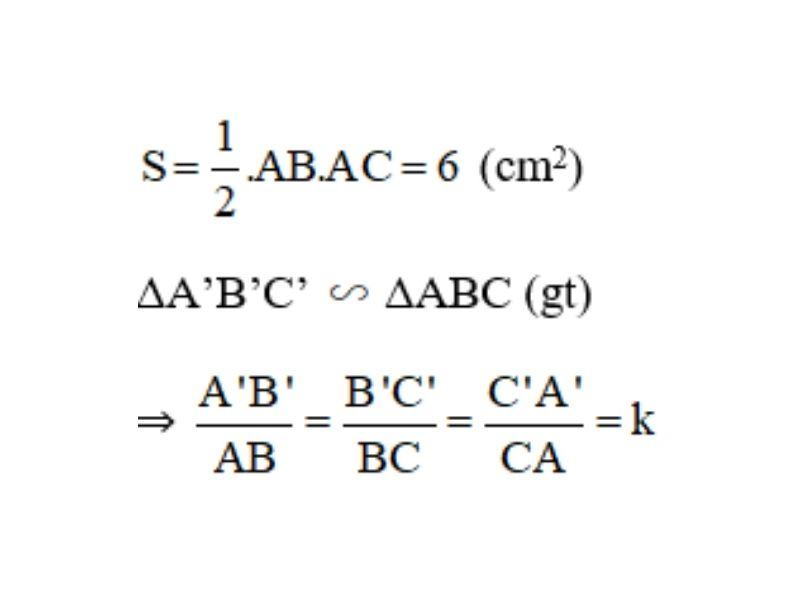
(với k là tỉ số đồng dạng).
Lại có tỉ số diện tích bằng bình phương tỉ số đồng dạng
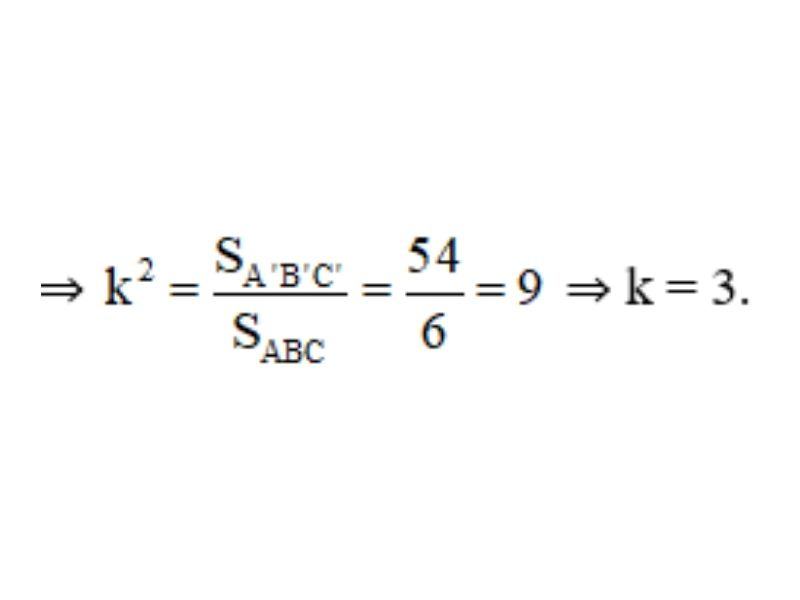
⇒ A’B’ = 3.AB = 3.3 = 9 (cm)
B’C’ = 3.BC = 3.5 = 15 (cm)
C’A’ = 3.CA = 3.4 = 12 (cm)
Vậy độ dài ba cạnh của tam giác lần lượt là 9cm, 12cm, 15cm.
Bài 48 trang 84 SGK Toán 8 tập 2
Câu hỏi: Bóng của cột điện trên mặt đất có độ dài là 4,5m. Cùng thời điểm đó, một thanh sắt cao 2,1m cắm vuông góc với mặt đất có bóng dài 0,6m. Tính chiều cao của cột điện.
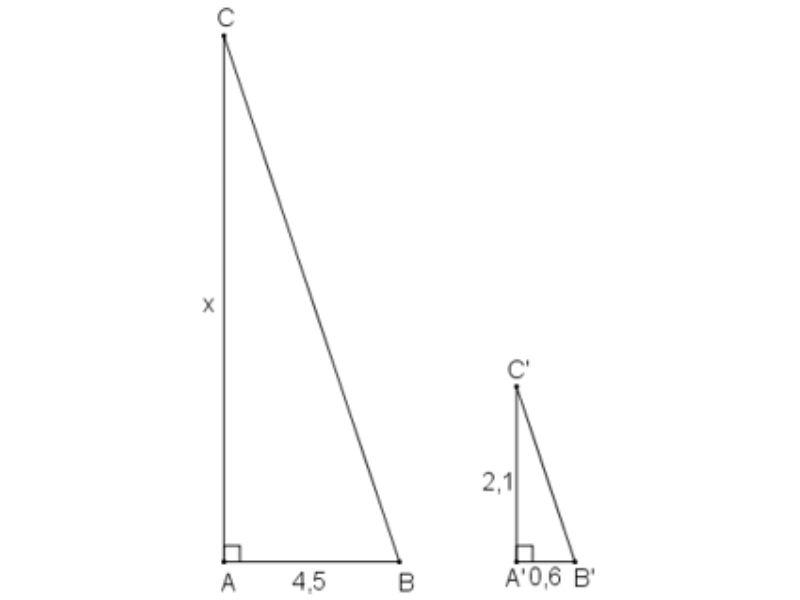
Trả lời:
Gọi chiều cao cột điện là x (m); (x > 0).
Giả sử cột điện là AC, có bóng trên mặt đất là AB.
Thanh sắt là A’C’, có bóng trên mặt đất là A’B’.
Vì cột điện và thanh sắt đều vuông góc với mặt đất nên hai tam giác ABC và A’B’C’ đều là tam giác vuông.
Vì cùng một thời điểm tia sáng tạo với mặt đất một góc bằng nhau.
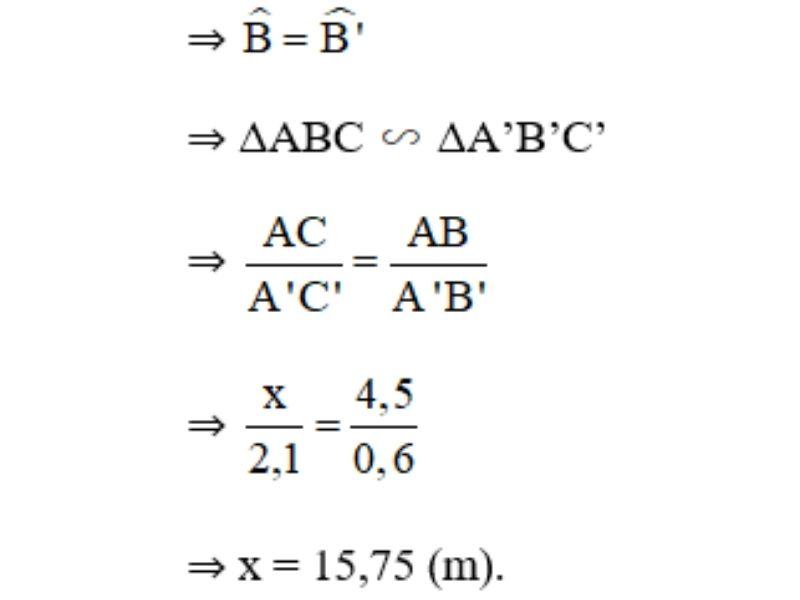
Vậy cột điện cao 15,75m.
Toàn bộ những thông tin trên là lý thuyết và bài tập áp dụng về các trường hợp đồng dạng của tam giác vuông. Mong rằng bài viết của Mas.edu.vn sẽ giúp bạn giải bài tập toán hình lớp 8 dễ dàng hơn. Hẹn gặp bạn trong những bài viết tiếp theo của Mas.edu.vn.
Trong bài viết này, chúng ta đã trình bày về các trường hợp đồng dạng của tam giác vuông cần nhớ. Chúng ta đã tìm hiểu về các quy tắc đồng dạng tam giác, chứng minh cho các trường hợp đặc biệt và cung cấp ví dụ minh họa cho mỗi trường hợp.
Tam giác vuông là một dạng đặc biệt của tam giác. Việc nắm vững và nhớ các trường hợp đồng dạng của tam giác vuông là một yêu cầu cần thiết trong việc giải quyết các bài toán hình học.
Các trường hợp đồng dạng của tam giác vuông bao gồm:
1. Quy tắc cạnh-huyền-huyền: Điều này áp dụng khi tỉ lệ giữa cạnh góc vuông và cạnh huyền của hai tam giác vuông là như nhau.
2. Quy tắc cạnh-cạnh-cạnh: Điều này áp dụng khi tỉ lệ giữa các cạnh của hai tam giác vuông là như nhau.
3. Quy tắc với cạnh-góc-cạnh: Điều này áp dụng khi tỉ lệ giữa cạnh góc vuông và hai cạnh không góc vuông của hai tam giác vuông là như nhau.
Việc nhớ và áp dụng đúng các trường hợp này sẽ giúp chúng ta giải quyết các bài toán hình học một cách hiệu quả và chính xác. Nắm vững các quy tắc đồng dạng tam giác là một kỹ năng cần thiết không chỉ trong học tập mà còn trong cuộc sống hàng ngày.
Nhờ vào việc tìm hiểu và áp dụng các trường hợp đồng dạng của tam giác vuông, chúng ta có thể dễ dàng xác định các độ dài cạnh, các góc, hay các định lý liên quan trong một bài toán. Điều này đồng thời giúp chúng ta hiểu sâu hơn về tính chất và cách vận dụng các đồng dạng của tam giác vuông.
Trong tương lai, việc nắm bắt và nhớ các trường hợp đồng dạng của tam giác vuông sẽ tiếp tục phát huy vai trò quan trọng trong các bài toán hình học, cũng như trong việc xây dựng cơ sở kiến thức toán học cho việc học tập và nghiên cứu.
Cảm ơn bạn đã xem bài viết Các trường hợp đồng dạng của tam giác vuông cần nhớ tại Mas.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Tam giác vuông cân
2. Tam giác vuông đều
3. Tam giác vuông nhọn góc
4. Tam giác vuông tù góc
5. Tam giác vuông bình thường
6. Tam giác vuông có cạnh gần bằng nhau
7. Tam giác vuông có cạnh lớn hơn nhau
8. Tam giác vuông có 2 cạnh bằng nhau
9. Tam giác vuông có 2 góc bằng nhau
10. Tam giác vuông có 2 cạnh vuông góc
11. Tam giác vuông có đường cao xuống cạnh huyền
12. Tam giác vuông có đường cao xuống cạnh góc nhọn
13. Tam giác vuông có đường trung tuyến vuông góc
14. Tam giác vuông có đường trung tuyến gắn tam giác
15. Tam giác vuông có đường phân giác góc vuông.