Bạn đang xem bài viết Các trường hợp bằng nhau của tam giác vuông Toán lớp 7 tại Mas.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Tam giác vuông là một khái niệm hết sức quen thuộc trong môn Toán lớp 7. Điểm đặc biệt của tam giác vuông chính là các cạnh của nó được định nghĩa theo quan hệ bằng nhau của các đường gọi tới đỉnh góc vuông. Trong bài viết này, chúng ta sẽ tìm hiểu về các trường hợp bằng nhau của tam giác vuông, tập trung vào dạng tam giác vuông cân và tam giác vuông đều.
Tam giác vuông cân là một tam giác vuông mà hai cạnh góc vuông cân bằng nhau. Đây là một dạng tam giác đặc biệt, khiến cho mỗi góc nhọn trong tam giác này đều có giá trị bằng 45 độ. Nhờ đặc điểm này mà tam giác vuông cân thường được sử dụng trong nhiều bài toán, giúp các em học sinh rèn kỹ năng giải các bài toán liên quan đến tam giác vuông.
Ngoài ra, tam giác vuông đều cũng là một trường hợp đặc biệt khác mà chúng ta sẽ tìm hiểu trong bài viết này. Tam giác vuông đều là một tam giác có cả ba cạnh và ba góc đều bằng nhau, mỗi góc trong tam giác này đều có giá trị bằng 60 độ. Tam giác vuông đều là một khái niệm quan trọng, vì tính nguyên tắc và tính đẹp của nó, cũng như ứng dụng trong nhiều bài toán thực tế.
Việc hiểu rõ về các trường hợp bằng nhau của tam giác vuông không chỉ giúp chúng ta làm quen với các dạng tam giác đặc biệt này mà còn giúp chúng ta áp dụng kiến thức này vào việc giải các bài toán, tăng cường khả năng phân tích và suy luận toán học. Bài viết này sẽ giúp các em hiểu rõ hơn về các trường hợp bằng nhau của tam giác vuông và thấy được ý nghĩa của chúng trong cuộc sống hàng ngày.
Các trường hợp bằng nhau của tam giác vuông là kiến thức vô cùng hữu ích trong chương trình Toán lớp 7. Mời các bạn đọc giả cùng Mas.edu.vn tóm tắt lý thuyết cơ bản và áp dụng giải một số bài tập nhé!
Danh Mục Bài Viết
Hai tam giác bằng nhau là gì?
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Để kí hiệu sự bằng nhau của tam giác ABC và tam giác DEF, ta có thể viết: ΔABC = ΔDEF
Các trường hợp bằng nhau của tam giác vuông
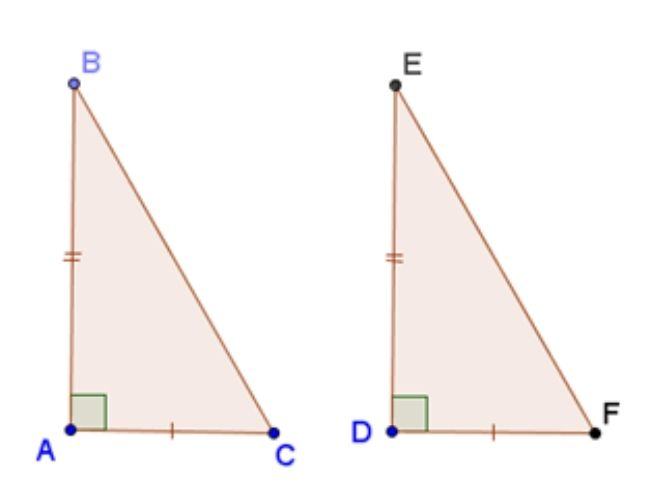
Hai cạnh góc vuông
Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (cạnh – góc – cạnh).
Ví dụ minh họa:
Xét hai tam giác ABC và DEF có:
AB = DE
AC = DF
⇒ Δ ABC = ΔDEF (hai cạnh góc vuông).
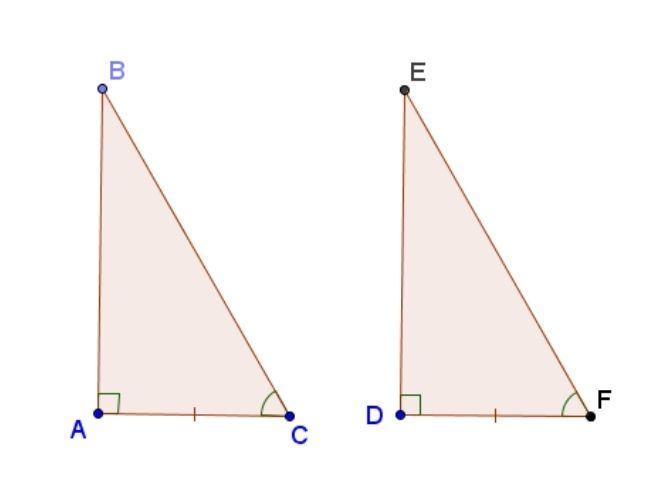
Cạnh góc vuông và góc nhọn kề cạnh đó
Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc ).
Ví dụ minh họa:
Xét hai tam giác ABC và DEF có:
AC = DF
Góc C = góc F
⇒ Δ ABC = ΔDEF (cạnh góc vuông – góc nhọn).
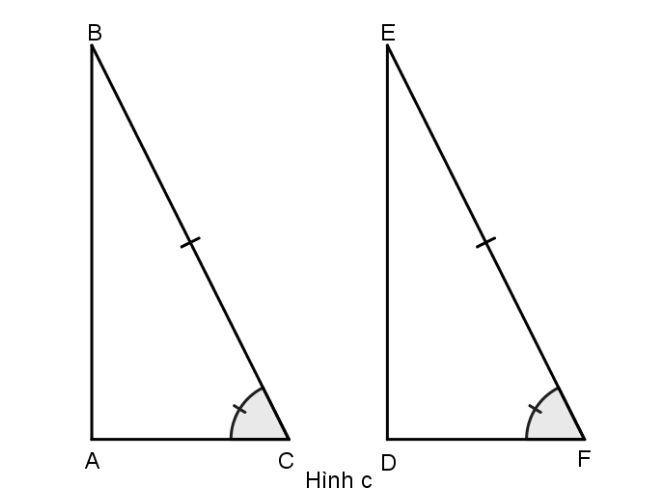
Cạnh huyền – Góc nhọn
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc).
Ví dụ minh họa:
Xét hai tam giác ABC và EDF có:
BC = EF
Góc B = góc E
⇒ Δ ABC = ΔDEF (cạnh huyền – góc nhọn).
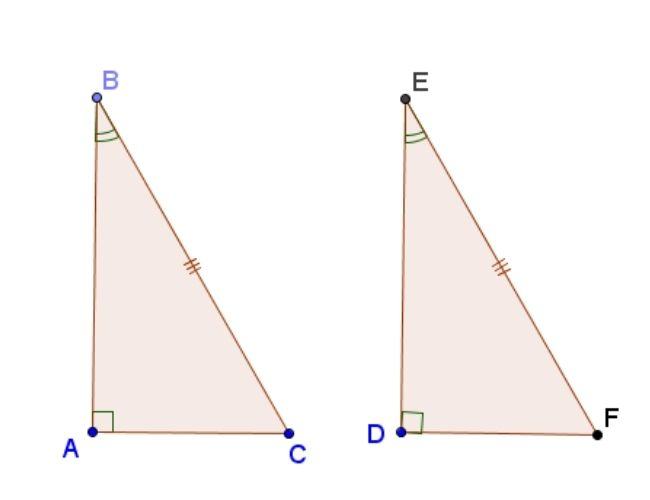
Cạnh huyền – Cạnh góc vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Ví dụ minh họa:
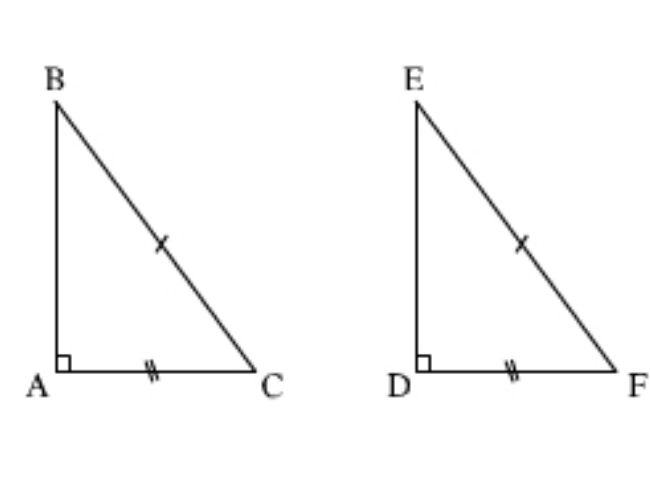
Xét hai tam giác ABC và DEF có:
AC = DF
BC = EF
⇒ Δ ABC = ΔDEF (cạnh huyền – cạnh góc vuông).
Xem thêm:
- Công thức tính cạnh huyền tam giác vuông đầy đủ nhất
- Các trường hợp đồng dạng của tam giác vuông cần nhớ
- Tính chất trực tâm là gì? 5 tính chất cơ bản trong tam giác
Bài tập trường hợp bằng nhau của tam giác vuông
Câu 1 bài 8 trang 135 SGK Toán lớp 7 tập 1
Trên mỗi hình 143, 144, 145 có các tam giác vuông nào bằng nhau? Vì sao?
Trả lời:
Hình 143:
Xét ΔABH vuông tại H và ΔACH vuông tại H có:
AH cạnh chung
BH = CH (giả thiết)
⇒ ΔABH = ΔACH (hai cạnh góc vuông).
Hình 144:
Xét ΔDKE vuông tại K và ΔDKF vuông tại F có:
DK cạnh chung
Góc EDK = góc FDK
⇒ ΔDKE = ΔDKF (cạnh góc vuông – góc nhọn kề).
Hình 145:
Xét ΔOMI vuông tại M và ΔONI vuông tại N có:
OI chung
Góc MOI = góc NOI (giả thiết)
⇒ ΔOMI = ΔONI (cạnh huyền – góc nhọn).
Câu 2 bài 8 trang 136 SGK Toán lớp 7 tập 1
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (hình 147). Chứng minh rằng ΔAHB = ΔAHC (giải bằng 2 cách).
Trả lời:
Cách 1:
Tam giác ABC cân tại A nên góc B = góc C và AB = AC (tính chất tam giác cân).
Xét hai tam giác AHB và AHC đều vuông tại H, có:
AB = AC (chứng minh trên)
Góc B = góc C (chứng minh trên)
⇒ ΔAHB = ΔAHC (cạnh huyền – góc nhọn).
Cách 2:
Xét hai tam giác vuông AHB và AHC có:
AB = AC (chứng minh trên)
AH cạnh chung
⇒ ΔAHB = ΔAHC (cạnh huyền – cạnh góc vuông).
Câu 64 trang 136 SGK Toán lớp 7 tập 1
Các tam giác vuông ABC và DEF có góc A = góc D = 90 độ, AC = DF. Hãy bổ sung thêm một điều kiện bằng nhau để ΔABC = ΔDEF
Trả lời:
Trường hợp 1: ΔABC=ΔDEF theo trường hợp hai cạnh góc vuông.
Xét hai tam giác vuông ABC và DEF có:
AC = DF (giả thiết)
Bổ sung thêm điều kiện AB = DE thì ΔABC = ΔDEF (hai cạnh góc vuông).
Trường hợp 2: ΔABC = ΔDEF theo trường hợp cạnh góc vuông – góc nhọn kề.
Xét hai tam giác vuông ABC và DEF có:
AC = DF (giả thiết)
Bổ sung thêm điều kiện góc C = góc F thì ΔABC = ΔDEF (cạnh góc vuông – góc nhọn kề).
Trường hợp 3: ΔABC = ΔDEF theo trường hợp cạnh huyền cạnh góc vuông.
Xét hai tam giác vuông ABC và DEF có:
AC = DF (giả thiết)
Bổ sung thêm điều kiện BC = EF thì ΔABC = ΔDEF (cạnh huyền – cạnh góc vuông).
Trên đây là tất tần tật kiến thức về các trường hợp bằng nhau của tam giác vuông. Hi vọng bài viết này của Mas.edu.vn hữu ích cho các bạn. Đừng quên ủng hộ Mas.edu.vn ở những chủ đề tiếp theo nhé!
Trong bài viết này, chúng ta đã tìm hiểu về các trường hợp bằng nhau của tam giác vuông trong môn Toán lớp 7. Các trường hợp này gồm có: hai góc nhọn bằng nhau, hai cạnh góc vuông bằng nhau và hai cạnh nhọn góc bằng nhau.
Đầu tiên, chúng ta đã xem xét về hai góc nhọn bằng nhau trong tam giác vuông. Chúng ta đã chứng minh rằng nếu hai góc nhọn bằng nhau, thì hai cạnh nhọn góc tương ứng cũng bằng nhau. Điều này được chứng minh bằng cách sử dụng định lí cộng góc trong tam giác và tính chất của góc vuông.
Tiếp theo, chúng ta đã xét về trường hợp hai cạnh góc vuông bằng nhau trong tam giác vuông. Chúng ta đã chứng minh rằng nếu hai cạnh góc vuông bằng nhau, thì hai góc nhọn tương ứng cũng bằng nhau. Điều này được chứng minh bằng cách sử dụng định lí cộng góc trong tam giác và tính chất của góc vuông.
Cuối cùng, chúng ta đã xét về trường hợp hai cạnh nhọn góc bằng nhau trong tam giác vuông. Chúng ta đã chứng minh rằng nếu hai cạnh nhọn góc bằng nhau, thì hai góc nhọn tương ứng cũng bằng nhau. Điều này được chứng minh bằng cách sử dụng định lí cộng góc trong tam giác và tính chất của góc vuông.
Tổng kết lại, các trường hợp bằng nhau của tam giác vuông là các trường hợp mà hai góc nhọn, hai cạnh góc vuông hoặc hai cạnh nhọn góc của tam giác bằng nhau. Những trường hợp này có thể được chứng minh bằng cách sử dụng các định lí cộng góc và tính chất của góc vuông. Việc hiểu về những trường hợp này đóng vai trò quan trọng trong việc giải các bài toán liên quan đến tam giác vuông và phát triển khả năng giải quyết vấn đề của học sinh.
Cảm ơn bạn đã xem bài viết Các trường hợp bằng nhau của tam giác vuông Toán lớp 7 tại Mas.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Tam giác vuông
2. Cạnh huyền
3. Cạnh góc vuông
4. Tỉ lệ
5. Đáy đồng dạng
6. Đồng dạng
7. Hình học
8. Phép biến đổi
9. Tính chất tam giác
10. Góc vuông
11. Chiều cao
12. Điều kiện bằng nhau của tam giác
13. Hình học giải tích
14. Đại số hình học
15. Bằng nhau.