Bạn đang xem bài viết Cách tính diện tích hình tam giác? Bài tập minh họa tại Mas.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Hình tam giác là một trong những hình học cơ bản được sử dụng rộng rãi trong toán học và các lĩnh vực khác. Để tính diện tích của một hình tam giác, chúng ta cần áp dụng một công thức đơn giản. Trước khi đi vào bài tập minh họa, hãy cùng tôi tìm hiểu về cách tính diện tích hình tam giác.
Diện tích hình tam giác được tính bằng một phép nhân đơn giản, dựa trên độ dài hai cạnh góc ôppôsit (opposite). Công thức cụ thể là: diện tích = 1/2 x độ dài cạnh a x độ dài cạnh b x sin góc ôppôsit (sin opposite angle). Để hiểu rõ hơn về cách áp dụng công thức này, chúng ta hãy xem qua một ví dụ minh họa.
Giả sử chúng ta có một tam giác ABC, trong đó cạnh a = 5 cm, cạnh b = 7 cm và góc ôppôsit cạnh a có giá trị 45 độ. Để tính diện tích tam giác này, ta sẽ sử dụng công thức đã nêu trên: diện tích = 1/2 x 5 cm x 7 cm x sin 45 độ.
Thực hiện tính toán, ta có: diện tích = 1/2 x 5 cm x 7 cm x 0.7071 ≈ 17.6775 cm².
Do đó, diện tích của tam giác ABC là khoảng 17.6775 cm².
Bài tập minh họa trên đã giúp chúng ta thấy rõ công thức tính diện tích hình tam giác và cách áp dụng nó vào thực tế. Hi vọng rằng sau bài viết này, việc tính diện tích hình tam giác sẽ trở nên dễ dàng và thú vị hơn đối với bạn. Hãy chú ý và luyện tập thường xuyên để nắm vững công thức này và áp dụng vào những bài tập khác nhau.
Diện tích tam giác là một kiến thức được áp dụng khá nhiều trong Toán học và đời sống. Mỗi hình tam giác khác nhau sẽ có các công thức khác nhau. Vậy cách tính diện tích hình tam giác như thế nào? Hãy tham khảo bài viết sau đây của Mas.edu.vn nhé!
Danh Mục Bài Viết
Hình tam giác là gì?
Hình tam giác là gì?
Hình tam giác là hình hai chiều phẳng có 3 đỉnh là ba điểm không nằm trên một đường thẳng. Hình tam giác có ba cạnh là ba đoạn thẳng nối các đỉnh lại với nhau.
Ngoài ra, hình tam giác là đa giác có số cạnh ít nhất là 3 cạnh. Hình tam giác luôn là một đa giác đơn hoặc là đa giác lồi. Tổng số đo các góc trong một hình tam giác luôn bằng 180 độ.
Hình tam giác được biết đến là một loại hình cơ bản trong hình học.
Phân loại các hình tam giác
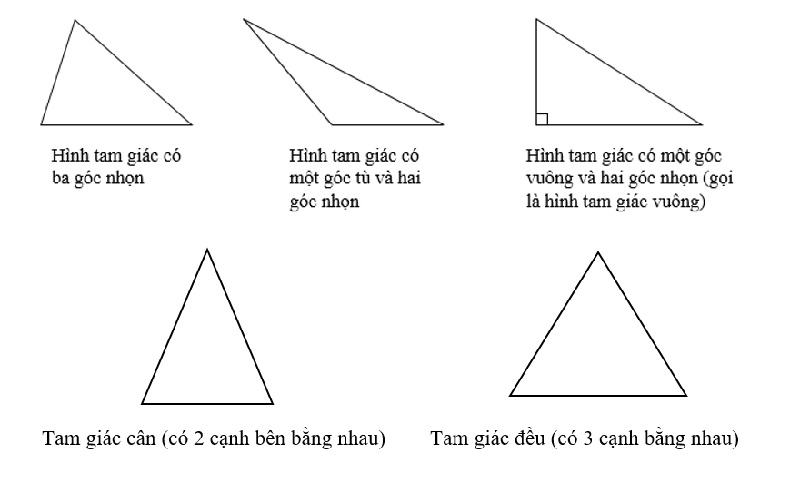
Hình tam giác là một loại hình cơ bản trong kiến thức Toán học. Có các loại hình tam giác sau:
Tam giác thường
Đây là loại tam giác cơ bản nhất. Tam giác thường có độ dài các cạnh khác nhau. Và có số đo của các góc cũng khác nhau. Tam giác thường cũng có thể bao gồm các trường hợp đặc biệt của một tam giác.
Tam giác cân
Tam giác cân là tam giác có hai cạnh bên bằng nhau. Đỉnh của tam giác chính là giao điểm của hai cạnh bên. Góc được tạo bởi đỉnh được gọi là góc ở đỉnh.
Bên cạnh đó hai góc còn lại gọi là góc ở đáy. Tam giác cân có tính chất là hai góc ở đáy thì bằng nhau.
Tam giác đều
Tam giác đều là tam giác có ba góc bằng nhau. Mỗi góc có số đo là 60 độ. Ngoài ra, cả ba cạnh của tam giác đều bằng nhau. Tam giác đều là trường hợp đặc biệt của tam giác cân.
Tam giác vuông
Tam giác vuông là tam giác có một góc bằng 90 độ. Trong tam giác vuông, cạnh đối diện với góc vuông được gọi là cạnh huyền.
Cạnh huyền có độ dài lớn nhất trong ba cạnh. Hai cạnh còn lại được gọi là cạnh góc vuông.
Tam giác vuông cân
Tam giác vuông cân là tam giác vừa vuông vừa cân. Tam giác vuông cân có một góc bằng 90 độ. Hai góc còn lại của tam giác bằng 45 độ.
Tam giác nhọn
Tam giác nhọn là tam giác có ba góc đều nhỏ hơn 90 độ. Hoặc tất cả các góc ngoài lớn hơn 90 độ.
Tam giác tù
Tam giác tù là tam giác có một góc lớn hơn 90 độ.
Cách tính diện tích hình tam giác
Cách tính diện tích hình tam giác thường
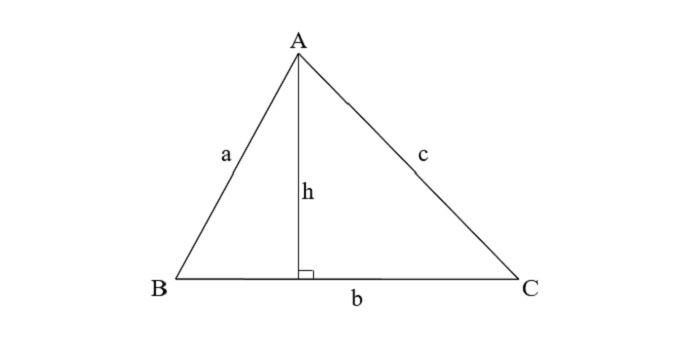
Tính diện tích hình tam giác thường bằng cách nhân chiều cao với độ dài đáy. Sau đó lấy kết quả tìm được chia cho hai.
Nói cách khác cách tính diện tích hình tam giác thường bằng một phần hai tích của chiều cao và độ dài đáy. Công thức tính diện tích tam giác thường như sau:
S= (a x h)/2
Trong đó:
- S là diện tích tam giác thường.
- a là độ dài đáy.
- h là chiều cao.
Bài tập minh họa cho công thức cách tính diện tích hình tam giác thường
Bài tập 1: Tính diện tích hình tam giác có
a) Độ dài đáy là 15cm và chiều cao là 12cm
b) Độ dài đáy là 6m và chiều cao là 4,5m
Trả lời:
a) Diện tích của hình tam giác là:
(15 x 12) : 2 = 90 (cm2)
Đáp số: 90cm2
b) Diện tích của hình tam giác là:
(6 x 4,5) : 2 = 13,5 (m2)
Đáp số: 13,5m2
Bài tập 2: Cho một hình tam giác ABC, trong đó có chiều cao nối từ đỉnh xuống đáy BC bằng 3cm, chiều dài đáy BC bằng 6cm. Tính diện tích tam giác thường ABC?
Trả lời:
Diện tích tam giác ABC là:
(a x h)/ 2 = (6×3)/2= 9 cm2
Cách tính diện tích hình tam giác vuông
Cách tính diện tích hình tam giác vuông cũng giống như cách tính diện tích hình tam giác thường. Đó là bằng một phần hai tích của chiều cao với độ dài đáy.
Công thức tính diện tích tam giác vuông như sau:
S= (a x h)/2
Trong đó:
- S là diện tích tam giác vuông.
- a là độ dài đáy của hình tam giác vuông.
- h là chiều cao của tam giác vuông.
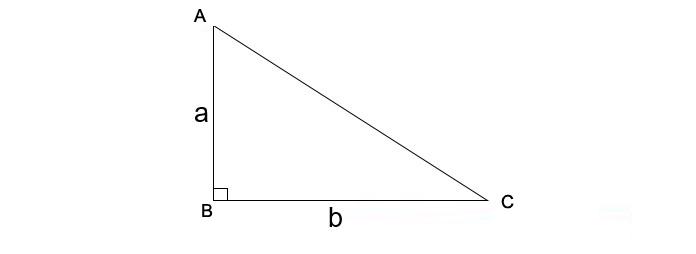
Tuy nhiên, công thức cách tính diện tích hình tam giác vuông sẽ dễ hơn so với tam giác thường. Vì chiều cao của tam giác vuông sẽ tương ứng với một cạnh góc vuông. Còn chiều dài đáy sẽ ứng với cạnh góc vuông còn lại.
Bài tập minh họa cho công thức cách tính diện tích hình tam giác vuông:
Bài tập 1: Tính diện tích của tam giác vuông có:
a) Hai cạnh góc vuông lần lượt là 3cm và 4cm
b) Hai cạnh góc vuông lần lượt là 6m và 8m
Trả lời:
a) Diện tích của hình tam giác là:
(3 x 4) : 2 = 6 (cm2)
Đáp số: 6cm2
b) Diện tích của hình tam giác là:
(6 x 8) : 2 = 24 (m2)
Đáp số: 24m2
Bài tập 2: Có một hình tam giác vuông ABC, vuông góc nhau tại điểm B, chiều dài cạnh đáy BC là 5 cm, chiều cao là 2 cm. Hỏi diện tích của hình tam giác vuông ABC bằng bao nhiêu?
Trả lời:
Diện tích tam giác vuông ABC là:
(5 x 2)/2 = 5cm2
Đáp số: 5cm2
Bài tập 3: Cho hình tam giác vuông ABC có diện tích là 30cm2. Trong đó chiều cao của tam giác vuông là 2cm. Hỏi độ dài đáy của tam vuông ABC là bao nhiêu?
Trả lời:
Độ dài đáy của tam giác vuông ABC là:
(30 x 2)/2= 30cm
Đáp số: 30cm
Bài tập 4: Cho tam giác ABC vuông góc tại A, chu vi là 90cm. Cạnh AB bằng 4/3 cạnh AC, cạnh BC bằng 5/3 cạnh AC. Tính diện tích hình tam giác ABC ?
Trả lời:
Cạnh AC là 3 phần bằng nhau thì cạnh AB là 4 phần và cạnh BC là 5 phần như thế
Độ dài cạnh AB là:
90 : (3 + 4 + 5) x 4 = 30 (cm)
Độ dài cạnh AC là:
90 : (3 + 4 + 5) x 3 = 22,5 (cm)
Diện tích hình tam giác ABC là:
30 x 22,5 : 2 = 337,5 (cm2)
Đáp số: 337,5 cm2
Cách tính diện tích hình tam giác cân
Cũng tương tự như cách tính diện tích hình tam giác thường. Cách tính diện tích hình tam giác cân là lấy tích của chiều cao với độ dài đáy. Sau đó lấy kết quả chia cho hai.
Công thức cách tính diện tích hình tam giác cân là:
S= (a x h)/2
Trong đó:
- S là diện tích tam giác cân.
- a là độ dài đáy của tam giác cân.
- h là chiều cao của tam giác cân. Chiều cao của tam giác được hình thành bằng một đoạn thẳng bắt đầu từ đỉnh xuống cạnh đáy.
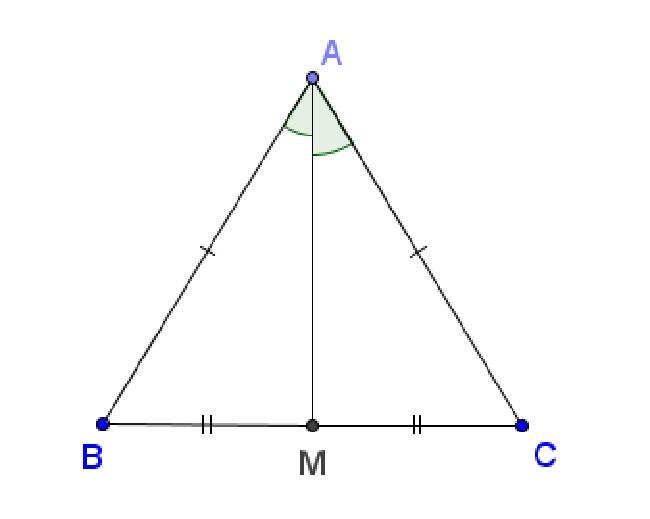
Bài tập minh họa cho cách tính diện tích hình tam giác cân:
Bài tập 1: Tính diện tích của tam giác cân có:
a) Độ dài cạnh đáy bằng 6cm và đường cao bằng 7cm
b) Độ dài cạnh đáy bằng 5m và đường cao bằng 3,2m
Trả lời:
a) Diện tích của hình tam giác là:
(6 x 7) : 2 = 21 (cm2)
Đáp số: 21cm2
b) Diện tích của hình tam giác là:
(5 x 3,2) : 2 = 8 (m2)
Đáp số: 8m2
Bài tập 2: Cho một tam giác cân ABC có chiều cao nối từ đỉnh A xuống đáy BC bằng 7cm, chiều dài đáy cho là 6cm. Hỏi diện tích của tam giác cân ABC bằng bao nhiêu?
Trả lời:
Diện tích tam giác cân ABC là:
(7 x 6)/2= 21cm2
Đáp số: 21cm2
Cách tính diện tích hình tam giác đều
Cách tính diện tích hình tam giác đều là lấy chiều cao nhân với độ dài đáy của tam giác đều. Sau đó lấy kết quả vừa tìm được chia cho hai.
Công thức cách tính diện tích hình tam giác đều như sau:
S= (a x h)/2
Trong đó:
- S là diện tích hình tam giác đều.
- a là độ dài đáy của hình tam giác đều.
- h là chiều cao của tam giác đều.
Ngoài công thức trên, do tam giác đều có tính chất là ba cạnh đều bằng nhau. Nên cách tính diện tích hình tam giác đều có thể được tính bằng công thức sau:
S = a^2 X (√3)/4
Trong đó:
- S là diện tích tam giác đều.
- a là độ dài các cạnh.
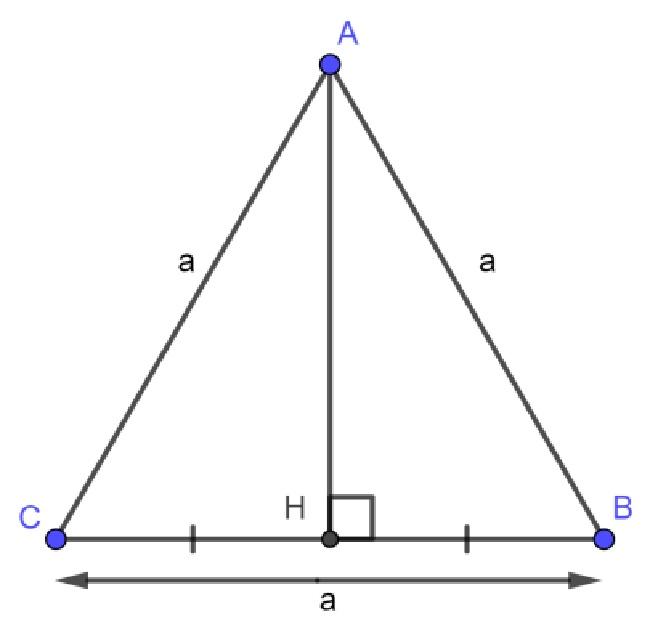
Bài tập minh họa cho công thức tính diện tích tam giác đều:
Bài tập 1: Tính diện tích của tam giác đều có:
a) Độ dài một cạnh tam giác bằng 6cm và đường cao bằng 10cm
b) Độ dài một cạnh tam giác bằng 4cm và đường cao bằng 5cm
Trả lời:
a) Diện tích hình tam giác là:
(6 x 10) : 2 = 30 (cm2)
Đáp số: 30cm2
b) Diện tích hình tam giác là:
(4 x 5) : 2 = 10 (cm2)
Đáp số: 10cm2
Bài tập 2: Có một tam giác đều ABC với chiều dài các cạnh bằng nhau là 9 cm, biết các góc của tam giác này đều bằng 60 độ. Hỏi diện tích tam giác đều ABC bằng bao nhiêu?
Trả lời:
Diện tích tam giác đều ABC là:
S = a2 x (√3)/4 = S = 92 x (√3)/4 = 81 x (√3)/4 = 35,07 cm2
Đáp số: 35,07 cm2
Cách tính diện tích hình tam giác vuông cân
Tương tự theo cách tính diện tích hình tam giác vuông. Mà đây là tam giác vuông cân nên có hai cạnh góc vuông bằng nhau.
Tính diện tích tam giác vuông cân bằng cách bình phương một cạnh. Sau đó lấy kết quả chia cho hai.
Công thức cách tính diện tích hình tam giác vuông cân như sau:
S = a^2/2
Trong đó:
- S là diện tích tam giác vuông cân.
- a là chiều dài một cạnh trong tam giác vuông cân.
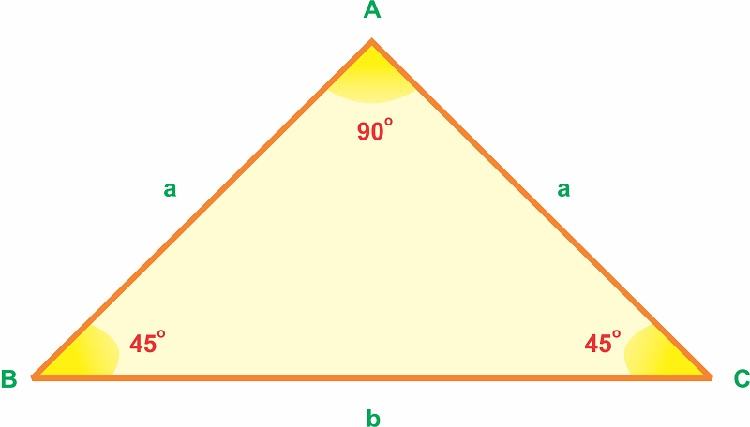
Bài tập minh họa cho công thức cách tính diện tích hình tam giác vuông cân:
Bài tập: Cho một hình tam giác vuông ABC và cân tại A. Có chiều dài một cạnh góc vuông là 6cm. Hãy tính diện tích tam giác ABC?
Trả lời:
Diện tích tam giác vuông cân ABC là:
6^2/2= 36/2= 18cm2
Đáp số: 18cm2
Cách tính diện tích hình tam giác trong hệ tọa độ Xoyz
Trong hình học không gian Xoyz, để tính diện tích tam giác người ta thường sử dụng tích có hướng để tính. Diện tích tam giác trong hệ tọa độ Xoyz được tính bằng cách lấy một phần hai của tích có hướng.
Công thức tính diện tích tam giác ABC trong hệ tọa độ Xoyz như sau:
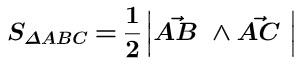
Bài tập minh họa cho công thức cách tính diện tích hình tam giác trong hệ tọa độ Xoyz:
Bài tập 1: Trong không gian Oxyz cho 3 điểm A(1;2;1), B(2;-1;3), C(5;2;-3). Tính diện tích của tam giác ABC.
Trả lời:
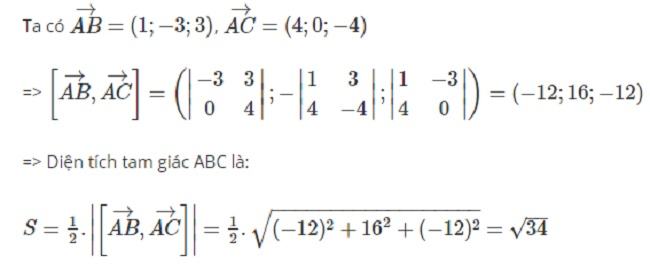
Bài tập 2: Cho ba điểm A(1;0;0), B(0;0;1), C(2;1;1).
a) Chứng minh rằng A, B, C là một đỉnh của tam giác
b) Tính diện tích tam giác ABC
Trả lời:

Xem thêm:
- Cách tính diện tích hình bình hành, ví dụ minh họa – Toán 4
- Cách tính chiều dài hình chữ nhật? Ví dụ giải bài tập lớp 5
- Cách tính diện tích hình thang – Giải bài tập Toán lớp 8
Những lưu ý khi tính diện tích hình tam giác
Khi tính diện tích tam giác, bạn cần lưu ý những điều cơ bản sau đây:
- Cần phải chú ý đến các đơn vị đo. Các đơn vị đo phải giống nhau. Nếu chưa giống nhau, bạn cần phải đưa về cùng một đơn vị đo rồi mới tính diện tích tam giác.
- Với các bài về diện tích, đơn vị đo phải tính theo mũ 2. Ví dụ như m2, cm2,…
Trên đây là toàn bộ thông tin liên quan đến cách tính diện tích hình tam giác. Hy vọng bài viết này của Mas.edu.vn đã giải đáp được toàn bộ những thắc mắc của bạn. Theo dõi Mas.edu.vn mỗi ngày để cập nhật thêm nhiều thông tin hay và bổ ích nhé!
Kết luận:
Trong bài viết này, chúng ta đã thảo luận về cách tính diện tích hình tam giác và cung cấp một số bài tập minh họa để định rõ hơn cách áp dụng công thức tính diện tích đối với các tam giác khác nhau.
Để tính diện tích hình tam giác, chúng ta có thể sử dụng công thức diện tích tam giác đều (S = (a^2 * sqrt(3))/4) hoặc công thức diện tích tam giác tổng quát (S = 1/2 * b * h), trong đó “a” là cạnh tam giác đều, “b” là độ dài của một cạnh và “h” là chiều cao tương ứng.
Bài tập minh họa đã cho thấy các ứng dụng thực tế của công thức diện tích tam giác. Chúng ta đã tính diện tích của một tam giác cân, một tam giác vuông và một tam giác bất kỳ.
Ngoài ra, chúng ta cũng đã thảo luận về một số phương pháp khác nhau để tính diện tích trong trường hợp không có đủ thông tin về cạnh và chiều cao của tam giác. Các phương pháp này bao gồm sử dụng định lý Pythagoras, định lý Hoà và công thức Heron.
Tổng kết lại, việc tính diện tích hình tam giác là một trong những kiến thức cơ bản trong học toán. Hiểu rõ công thức và ứng dụng của nó giúp chúng ta áp dụng vào thực tế và giải quyết các bài toán liên quan. Qua các bài tập minh họa, ta đã có cơ hội vận dụng kiến thức này và nâng cao kỹ năng trong việc tính toán diện tích tam giác.
Cảm ơn bạn đã xem bài viết Cách tính diện tích hình tam giác? Bài tập minh họa tại Mas.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Hình tam giác
2. Diện tích tam giác
3. Công thức tính diện tích tam giác
4. Tam giác đều
5. Tam giác vuông
6. Đường cao tam giác
7. Cạnh tam giác
8. Công thức Heron
9. Tính diện tích tam giác bằng đường cao
10. Tính diện tích tam giác bằng cạnh và góc
11. Tính diện tích tam giác bằng đa giác lồi
12. Tính diện tích tam giác bằng biểu thức Heron
13. Công thức tính diện tích tam giác vuông
14. Bài toán tính diện tích tam giác
15. Hình học tam giác