Bạn đang xem bài viết Đường trung tuyến là gì? Tính chất và công thức tính đường trung tuyến tại Mas.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Đường trung tuyến là một khái niệm quan trọng trong hình học trong tam giác. Nó là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện. Đường trung tuyến được xem như một “đường chia đôi” tam giác, chia thành hai phần bằng nhau và liên kết các điểm quan trọng trong tam giác với nhau.
Công thức tính đường trung tuyến của tam giác rất đơn giản. Đối với một tam giác ABC, đường trung tuyến từ đỉnh A sẽ là đoạn thẳng nối A với trung điểm của cạnh BC, và được kí hiệu là d_a. Tương tự, ta có đường trung tuyến từ đỉnh B là đoạn thẳng nối B với trung điểm của cạnh AC, và được kí hiệu là d_b. Cuối cùng, đường trung tuyến từ đỉnh C là đoạn thẳng nối C với trung điểm của cạnh AB, và được kí hiệu là d_c.
Đường trung tuyến có một số tính chất đáng chú ý. Đầu tiên, ba đường trung tuyến trong tam giác này đồng quy tại một điểm, gọi là trọng tâm của tam giác. Điều này có nghĩa là đường trung tuyến từ mỗi đỉnh đều cắt đường trung trực của cạnh đối diện tại một điểm duy nhất. Thứ hai, đường trung tuyến cũng chính là tia phân giác của góc ứng với đỉnh tương ứng. Điều này có nghĩa là đường trung tuyến chia đôi góc ứng với đỉnh và cắt nhau tại một điểm trên đường trung đoạn của cạnh đối diện.
Đường trung tuyến là một khái niệm quan trọng trong hình học tam giác và có nhiều ứng dụng thực tế. Hiểu rõ tính chất và công thức tính đường trung tuyến sẽ giúp chúng ta giải quyết một số bài toán hình học liên quan đến tam giác một cách dễ dàng và hiệu quả.
Trong toán học, đường trung tuyến trong tam giác là một trong những kiến thức cơ bản đối với học sinh cấp 2, cấp 3. Đường trung tuyến được vận dụng khá nhiều trong các bài hình học.
Do đó, việc hiểu được định nghĩa đường trung tuyến là gì và tính chất của nó rất quan trọng. Bài viết sau đây của Mas.edu.vn sẽ gửi đến bạn kiến thức liên quan đến đường trung tuyến.
Danh Mục Bài Viết
Đường trung tuyến là gì?
Trung tuyến là gì?
Trung tuyến trong tam giác là đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của đoạn đối diện. Mỗi tam giác đều có ba trung tuyến. Đối với tam giác cân và tam giác đều, mỗi trung tuyến của tam giác chia đôi các góc ở đỉnh với hai cạnh kề có chiều dài bằng nhau.
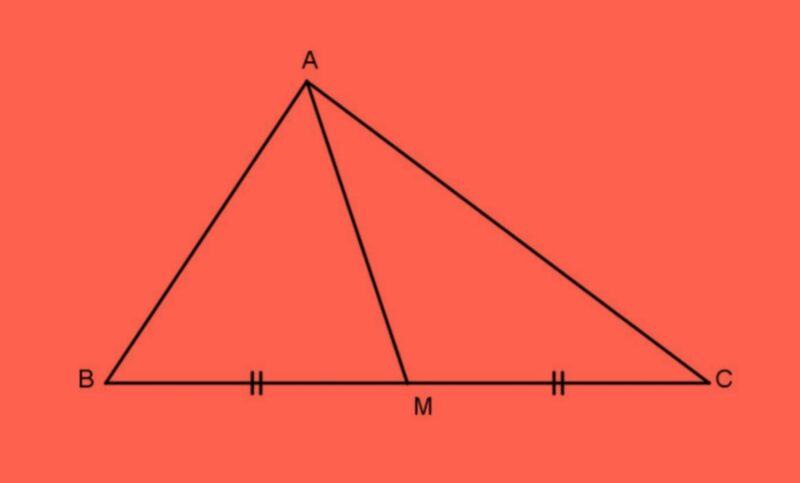
Đường trung tuyến là gì?
Đường trung tuyến của một đoạn thẳng là đường thẳng đi qua trung điểm của đoạn thẳng. Trong đó, trung điểm là điểm chia đoạn thẳng thành hai phần có độ dài bằng nhau.
Đường trung tuyến trong tam giác là đoạn thẳng nối từ đỉnh đến trung điểm của cạnh đối diện. Một tam giác có 3 đường trung tuyến.
Đường trung tuyến tiếng Anh là gì?
Đường trung tuyến tiếng Anh là median line. Sau đây là một số ví dụ về cụm từ median line:
- On its western end the line extends out along the 38th parallel to the median line between Korea and China. (Vào đầu phía tây của đường kéo dài dọc theo vĩ tuyến 38 đến đường trung tuyến giữa Triều Tiên và Trung Quốc.)
- The country has, however, stated that the EEZ between neighboring countries or countries that are opposite one another should be determined by consultation in accordance with the principle of an equidistant line or a median line. (Tuy nhiên, quốc gia này đã tuyên bố rằng vùng đặc quyền kinh tế giữa các quốc gia láng giềng hoặc các quốc gia đối diện nhau, nên được xác định bằng cách tham khảo ý kiến theo nguyên tắc của đường đẳng thức hoặc đường trung tuyến.)
Tính chất đường trung tuyến
Trong tam giác thường, đường trung tuyến có tính chất sau:
- Ba đường trung tuyến của một tam giác đồng quy tại một điểm, điểm đó được gọi là trọng tâm của tam giác.
- Khoảng cách từ trọng tâm của tam giác đến đỉnh bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó.
- Khoảng cách từ trọng tâm đến trung điểm của mỗi cạnh bằng 1/3 độ dài đường trung tuyến tương ứng với cạnh đó.
Tính chất đường trung tuyến trong tam giác cân
Trong tam giác cân, đường trung tuyến ứng với cạnh đáy thì vuông góc với cạnh đáy. Lúc này đường trung tuyến được xem là đường trung trực của cạnh đáy. Nó sẽ chia tam giác cân thành hai tam giác bằng nhau.
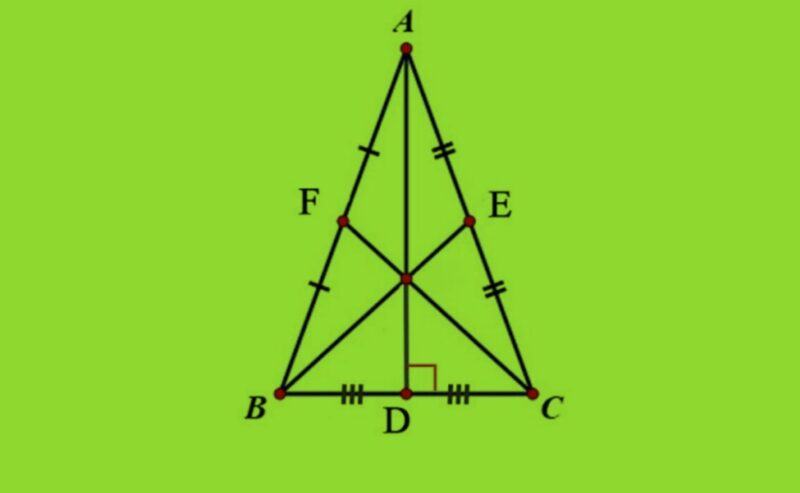
Đường trung tuyến ứng từ góc đỉnh của tam giác cân sẽ chia góc đỉnh thành hai góc bằng nhau. Trong trường hợp này, đường trung tuyến được coi là đường phân giác của góc đỉnh.
Tính chất đường trung tuyến trong tam giác vuông
Dưới đây là tính chất đường trung tuyến trong tam giác vuông. Mời độc giả của Mas.edu.vn cùng tham khảo:
- Trong tam giác vuông, trung tuyến ứng với cạnh huyền sẽ có chiều dài bằng nửa cạnh huyền.
- Một tam giác có trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.
- Đường trung tuyến của tam giác vuông có đầy đủ các tính chất của một đường trung tuyến tam giác thường.
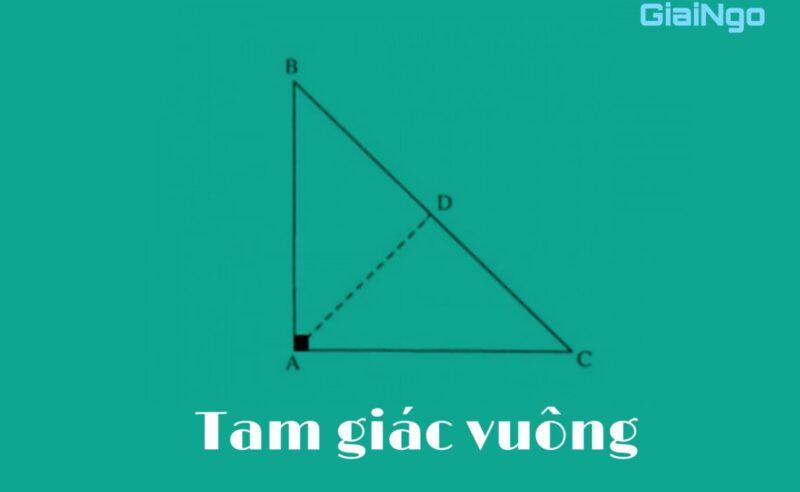
Trong tam giác vuông cân, đường trung tuyến từ góc vuông, ứng với cạnh huyền sẽ có các tính chất đường trung tuyến của tam giác vuông và tam giác cân. Điều này có nghĩa là nó sẽ có chiều dài bằng 1/2 cạnh huyền, vuông góc với cạnh huyền và chia góc vuông thành 2 góc có 450.
Tính chất đường trung tuyến trong tam giác đều
Nội dung sau sẽ giúp bạn tìm hiểu về tính chất đường trung tuyến trong tam giác đều:
- Ba đường trung tuyến của tam giác đều sẽ chia tam giác đó thành sáu tam giác có diện tích bằng nhau.
- Ba đường trung tuyến của tam giác đều có độ dài bằng nhau.
- Ba đường trung tuyến cũng đồng thời là ba đường trung trực và đường phân giác của tam giác đều.

- Trong tam giác đều, đường thẳng đi qua một đỉnh bất kỳ và đi qua trọng tâm của tam giác sẽ chia tam giác đó thành hai tam giác có diện tích bằng nhau.
- Có đầy đủ các tính chất của đường trung tuyến tam giác cân
Cách tính đường trung tuyến
Độ dài đường trung tuyến của một tam giác được tính thông qua độ dài các cạnh của tam giác và được tính bằng định lý Apollonnius:
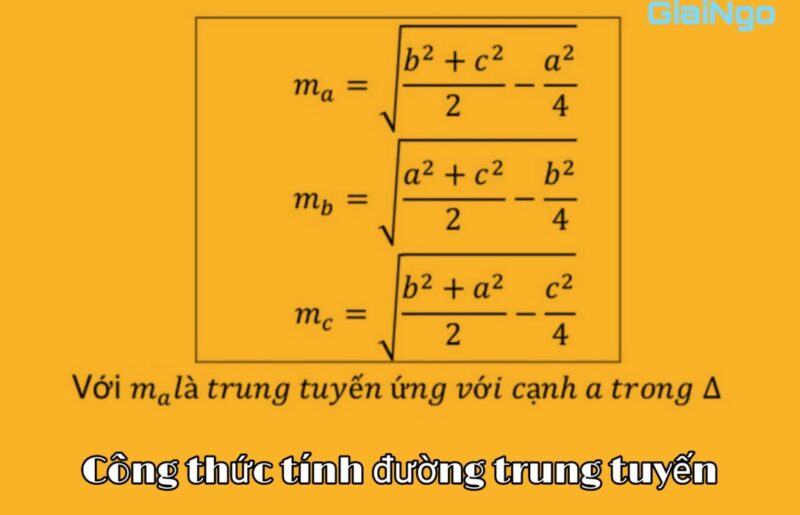
Trong đó:
- a, b, c: là các cạnh của tam giác.
- ma, mb, mc: là các đường trung tuyến của tam giác.
Bài viết hôm nay của Mas.edu.vn đã giúp bạn ôn lại định nghĩa đường trung tuyến là gì cùng những kiến thức liên quan. Hãy chia sẻ bài viết này để mọi người cùng biết nhé! Chúc độc giả của Mas.edu.vn có một ngày cuối tuần thật vui vẻ.
Trên thực tế, đường trung tuyến là một khái niệm quan trọng trong hình học và các khía cạnh liên quan đến tam giác. Đường trung tuyến là đường thẳng đi qua một điểm chính giữa một cạnh tam giác và điểm trung điểm của cạnh đối diện. Nó được gọi là “đường trung tuyến” vì nó chia cạnh đối diện làm hai phần có cùng chiều dài.
Điểm đặc biệt của đường trung tuyến là nó có một số tính chất quan trọng. Đầu tiên, đường trung tuyến luôn luôn đi qua trọng tâm của tam giác, điểm trung điểm còn là trọng tâm của tam giác, nên đường trung tuyến được coi là “đường đặc biệt”. Thứ hai, đường trung tuyến cắt một cạnh tam giác thành hai đoạn có cùng độ dài, mỗi đoạn có độ dài bằng nửa chiều dài cạnh đối diện. Điều này cũng có nghĩa là nếu có hai đường trung tuyến song song, thì tam giác đó là tam giác đều.
Công thức tính đường trung tuyến cũng rất đơn giản. Cho tam giác ABC, với M là trung điểm của cạnh AB. Đường trung tuyến từ đỉnh C đi qua trọng tâm G sẽ cắt cạnh AB tại một điểm N, ta có công thức tính tọa độ của điểm này là:
[N= left(frac{{A_x+B_x}}{2}, frac{{A_y+B_y}}{2}right)]
Với Ax, Ay là tọa độ điểm A, Bx, By là tọa độ điểm B. Tuy nhiên, ta cũng có thể tính đường trung tuyến từ đỉnh A hoặc B đến trọng tâm G bằng cách thực hiện công thức tương tự.
Tóm lại, đường trung tuyến là đường thẳng chia cạnh đối diện thành hai đoạn bằng nhau và luôn đi qua trọng tâm của tam giác. Nó là một thuật ngữ quan trọng trong hình học tam giác và tính chất của nó có thể được áp dụng trong nhiều bài toán và chứng minh.
Cảm ơn bạn đã xem bài viết Đường trung tuyến là gì? Tính chất và công thức tính đường trung tuyến tại Mas.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Đường trung tuyến
2. Đường nối trực giao
3. Đường trung tuyến trong tam giác
4. Tính chất của đường trung tuyến
5. Đường trung tuyến là đường nào?
6. Công thức tính đường trung tuyến
7. Định lý vị trí đường trung tuyến trong tam giác
8. Đặc điểm của đường trung tuyến
9. Mối quan hệ giữa đường trung tuyến và tâm đường tròn ngoại tiếp
10. Đường trung tuyến trong tam giác đều
11. Đường trung tuyến trong tam giác vuông
12. Đường trung tuyến trong tam giác cân
13. Phương trình đường trung tuyến trong tam giác
14. Đường trung tuyến và trung điểm
15. Mối quan hệ giữa đường trung tuyến và đường trung bình.