Bạn đang xem bài viết Hàm số đồng biến khi nào? Phương pháp xét đồng biến, nghịch biến tại Mas.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Hàm số là một khái niệm quan trọng trong toán học và có ứng dụng rộng rãi trong các lĩnh vực khác nhau. Trong quá trình nghiên cứu hàm số, một trong những khái niệm quan trọng cần được hiểu rõ là tính đồng biến và tính nghịch biến của hàm số.
Tính đồng biến và tính nghịch biến của hàm số cho ta biết về sự thay đổi của giá trị của hàm số khi biến đổi biến độc lập. Điều này rất hữu ích trong việc nghiên cứu sự biến thiên của hàm số, tìm vị trí của các điểm cực trị, và xác định giá trị lớn nhất hay nhỏ nhất của hàm số trên một khoảng xác định.
Phương pháp xét tính đồng biến và nghịch biến của hàm số cung cấp cho chúng ta một cách tiếp cận hệ thống và chính xác để phân tích tính chất của hàm số. Bằng cách phân tích biến đổi của hàm số và dựa vào sự thay đổi của đạo hàm, ta có thể xác định được điểm cực trị và xác định tính chất của hàm số trên một khoảng xác định.
Phương pháp này không chỉ đóng góp quan trọng cho nghiên cứu và ứng dụng của hàm số, mà còn giúp chúng ta hiểu rõ hơn về tính chất và mối quan hệ giữa các giá trị của hàm số trong các biến độc lập khác nhau.
Trong bài viết này, chúng ta sẽ tìm hiểu cách xác định tính đồng biến và tính nghịch biến của hàm số thông qua phương pháp xét đạo hàm. Chúng ta sẽ đi sâu vào cách tính đạo hàm của hàm số và áp dụng nó để xác định các khoảng đồng biến và nghịch biến của hàm số. Chúng ta cũng sẽ tìm hiểu về những trường hợp đặc biệt khi hàm số không đồng biến hoặc không nghịch biến.
Qua việc nắm vững phương pháp xét tính đồng biến và tính nghịch biến của hàm số, ta sẽ có thêm công cụ hữu ích trong quá trình giải quyết các bài toán liên quan đến hàm số.
Đồng biến, nghịch biến là tính chất quan trọng được vận dụng nhiều trong khảo sát hàm số. Nhiều bạn học sinh đặt câu hỏi hàm số đồng biến khi nào? Phương pháp xét đồng biến, nghịch biến là gì? Qua bài viết này của Mas.edu.vn sẽ giúp các bạn ôn tập kiến thức để vận dụng vào bài tập. Cùng đón đọc nhé!
Danh Mục Bài Viết
Khái niệm về sự đồng biến của hàm số
Cho K là một khoảng, một đoạn hoặc một nửa khoảng và y = f(x) là một hàm số xác định trên K.
Hàm số y = f(x) được gọi là đồng biến (tăng) trên K, nếu:
∀ x1, x2 ∊ K mà x1 < x2 thì f (x1) < f (x2)
Biểu diễn đồ thị hàm số là một đường đi lên. Hàm số đồng biến hoặc nghịch biến trên K còn gọi chung là hàm số đơn điệu trên K.
Hàm số đồng biến khi nào?
Hàm số f đồng biến trên K khi và chỉ khi:
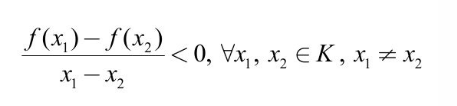
Điều kiện đủ để hàm số đồng biến
Cho hàm số f có đạo hàm trên K.
Nếu f'(x) > 0 với mọi x ∈ K thì hàm số f đồng biến trên K.
Phương pháp xét đồng biến và nghịch biến
Để xét tính đồng biến và nghịch biến của hàm số, ta cần áp dụng phương pháp sau:
- Tìm tập xác định
- Tính đạo hàm f'(x). Tìm các điểm xi (i= 1 , 2 ,…, n) mà tại đó f'(x) bằng 0 hoặc không xác định.
- Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
- Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Ví dụ tìm m để hàm số đồng biến trên khoảng nghịch biến trên khoảng
Dạng 1: Tìm m để hàm số đồng biến trên R, nghịch biến trên R.
Dạng toán này thường gặp với đa thức bậc 3. Chúng ta có công thức như sau:

Ví dụ:
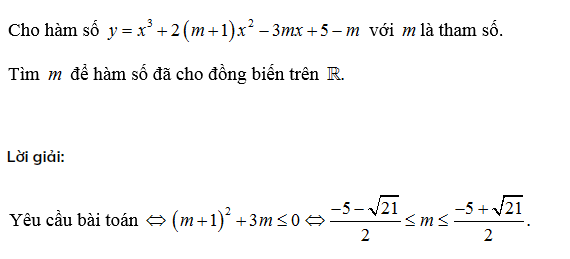
Dạng 2: Tìm m để hàm số đồng biến, nghịch biến trên từng khoảng xác định
Dạng này ta thường gặp ở hàm phân tuyến tính (hay hàm số phân thức bậc 1 trên bậc 1). Ta áp dụng công thức sau:

Ví dụ:

Dạng 3: Nhẩm được nghiệm của đạo hàm
Ví dụ:
Cho hàm số y = x³ – (m+1)x² – (m²-2m)x + 2020. Tìm m để hàm số nghịch biến trên khoảng (0;1).
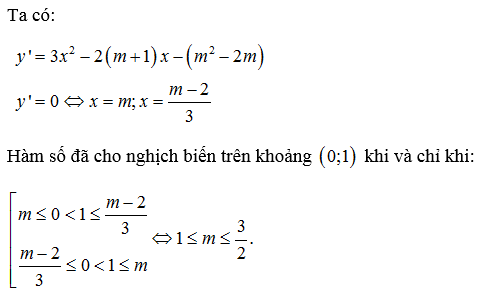
Dạng 4: Cô lập tham số m
Ví dụ:
Cho hàm số y = x³ + mx² + 2mx + 3. Tìm điều kiện của m để hàm số đồng biến trên khoảng (0;2).
Lời giải:
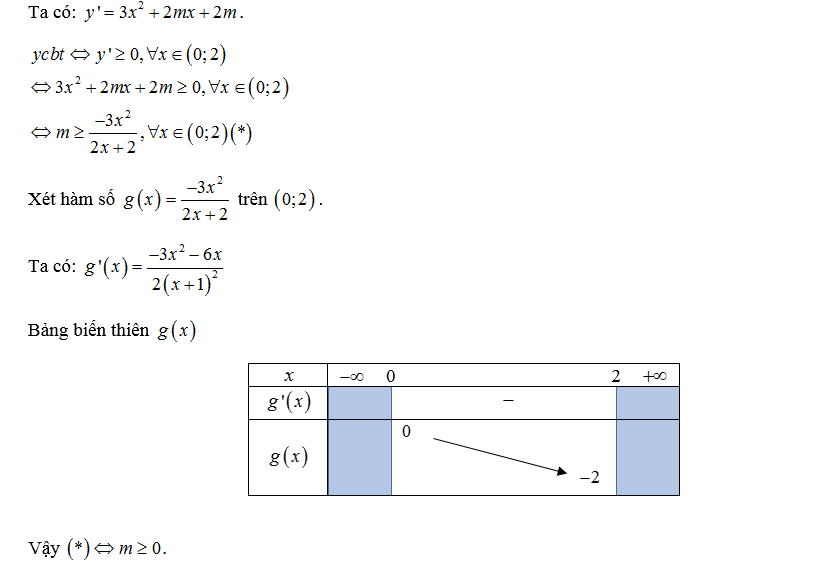
Dạng 5: Hàm phân tuyến tính đơn điệu trên khoảng cho trước
Nếu là hàm phân tuyến tính có tham số, trường hợp hàm số suy biến rất dễ xảy ra. Ta cần xét trường hợp hàm số suy biến thành hàm bậc nhất.
Trường hợp khác hàm suy biến thành hằng thì không cần xét vì hàm số này không phải hàm đơn điệu. Nếu xét hàm suy biến, có thể áp dụng công thức sau:

Ví dụ 1:
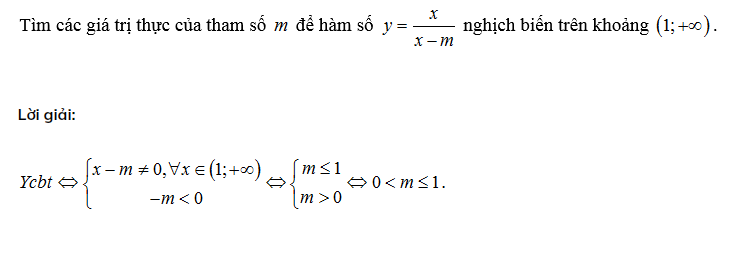
Ví dụ 2:
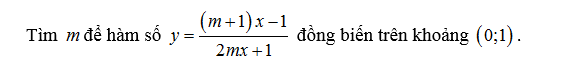
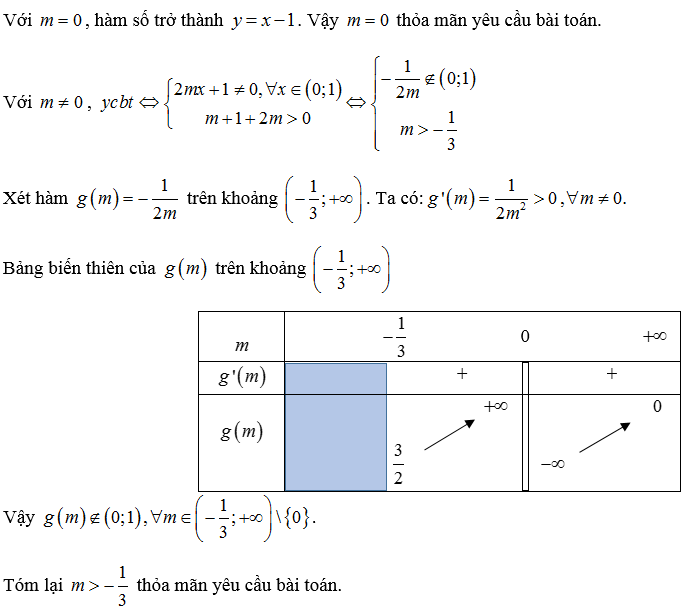
Trên đây là kiến thức về hàm số đồng biến khi nào, phương pháp giải và một số bài toán mẫu. Hy vọng có thể giúp bạn củng cố kiến thức và ôn tập tốt để làm tốt bài thi THPT quốc gia. Chúc các bạn thành công!
Trong toán học, hàm số là một quy tắc biến đổi ánh xạ giữa hai tập số. Khi nghiên cứu các hàm số, một trong những điều quan trọng để hiểu là hàm số có tính chất đồng biến hay không. Trong phạm vi bài viết này, chúng ta sẽ xem xét vấn đề này cũng như phương pháp xét đồng biến, nghịch biến của hàm số.
Hàm số được gọi là đồng biến trên một khoảng xác định nếu khi tăng hoặc giảm biến số độc lập, giá trị của hàm số tăng hoặc giảm theo cùng một hướng. Nghĩa là, nếu ta chọn hai giá trị x1 và x2 trong khoảng đó, trong đó x1 f(x2) nếu hàm số giảm. Hàm số sẽ không có tính chất đồng biến nếu tồn tại hai giá trị trong khoảng đó có f(x1) > f(x2) khi hàm số tăng và f(x1)
Cảm ơn bạn đã xem bài viết Hàm số đồng biến khi nào? Phương pháp xét đồng biến, nghịch biến tại Mas.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Hàm số đồng biến
2. Hàm số nghịch biến
3. Hàm số tăng
4. Hàm số giảm
5. Phương pháp xét đồng biến
6. Phương pháp xét nghịch biến
7. Đồ thị hàm số
8. Đặt điểm cực trị
9. Đặt điểm cực đại
10. Đặt điểm cực tiểu
11. Đồ thị hàm số đồng biến
12. Đồ thị hàm số nghịch biến
13. Đại lượng cục bộ
14. Điểm bậc cực đại
15. Điểm bậc cực tiểu