Bạn đang xem bài viết Hawngf ddawngr thuwcs – Bài tập về 7 hằng đẳng thức đáng nhớ tại Mas.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Hawngf ddawngr thuwcs là một chủ đề quan trọng trong toán học. Đây là một bài tập đòi hỏi kiến thức và khả năng giải quyết vấn đề của sinh viên. Trong bài viết này, chúng ta sẽ tìm hiểu về 7 hằng đẳng thức đáng nhớ và cách áp dụng chúng vào việc giải quyết các bài toán thực tế. Sự hiểu biết về những hằng đẳng thức này không chỉ giúp chúng ta làm giảm thời gian giải quyết các bài toán phức tạp mà còn giúp chúng ta hiểu sâu về những quy tắc cơ bản của toán học. Hãy cùng khám phá về các hằng đẳng thức này và ứng dụng của chúng trong thực tế.
HĐT (hằng đẳng thức) gồm 7 đẳng thức cơ bản nhất mà mỗi người học Toán cần phải nắm vững. Vậy có những hằng đẳng thức (hawngf ddawngr thuwcs) nào? Mời bạn tham khảo nội dung bài viết này của Mas.edu.vn nhé.
7 hằng đẳng thức đáng nhớ (hawngf ddawngr thuwcs)
Bình phương của một tổng
Đằng thức: (a + b)2 = a2 + 2 * a * b + b2
Diễn giải: Bình phương của một tổng bằng bình phương số thứ nhất, cộng với hai lần tích số thứ nhất và số thứ hai, cộng với bình phương số thứ hai.
Bình phương của một hiệu
Đẳng thức: (a – b)2 = a2 – 2 * a * b + b2
Diễn giải: Bình phương của một hiệu bằng bình phương số thứ nhất, trừ đi hai lần tích số thứ nhất và số thứ hai, cộng với bình phương số thứ hai.
Hiệu hai bình phương
Đẳng thức: a2 – b2 = (a – b) * (a + b)
Diễn giải: Hiệu hai bình phương bằng hiệu của số thứ nhất và số thứ hai nhân với tổng của số thứ nhất và số thứ hai.
Lập phương của một tổng
Đẳng thức: (a + b)3 = a3 + 3 * a2 * b + 3 * a * b2 + b3
Diễn giải: Lập phương của một tổng bằng lập phương của số thứ nhất, cộng ba lần tích bình phương của số thứ nhất với số thứ hai, cộng ba lần tích số thứ nhất với bình phương của số thứ hai, cộng lập phương của số thứ hai.
Đây là một dạng của hằng đẳng thức bậc 3.
Lập phương của một hiệu
Đẳng thức: (a – b)3 = a3 – 3 * a2 * b + 3 * a * b2 – b3
Diễn giải: Lập phương của một hiệu bằng lập phương của số thứ nhất trừ đi ba lần tích của bình phương số thứ nhất nhân cho số thứ hai, cộng với ba lần tích của số thứ nhất nhân với bình phương của số thứ hai, rồi sau đó trừ đi lập phương của số thứ hai.
Tổng hai lập phương
Đẳng thức: a3 + b3 = (a + b) * (a2 – a * b + b2)
Diễn giải: Tổng hai lập phương bằng tổng của số thứ nhất và số thứ hai Nhân với bình phương thiếu của hiệu.
Hiệu hai lập phương
Đẳng thức: a3 – b3 = (a – b) * (a2 + a * b + b2)
Diễn giải: Hiệu hai lập phương bằng hiệu của số thứ nhất và số thứ hai nhân với bình phương thiếu của tổng.
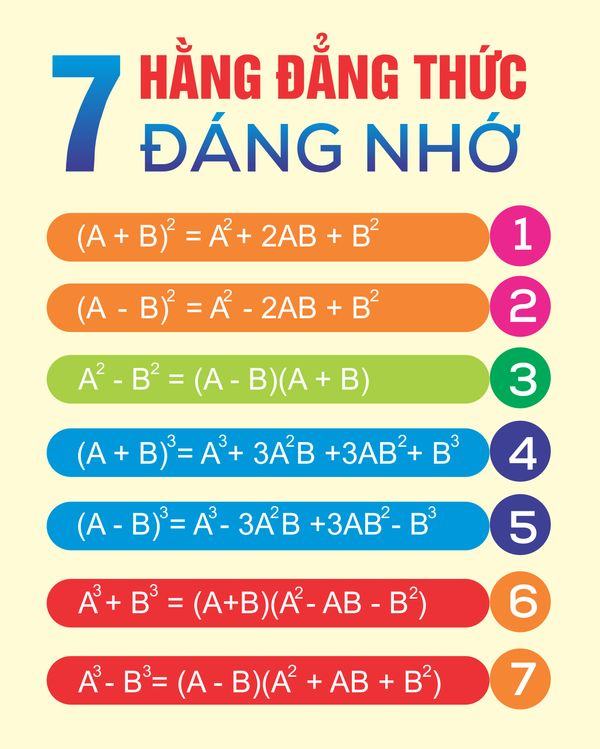
Cách ghi nhớ bảy hằng đẳng thức đáng nhớ hiệu quả
Dưới đây là 3 cách ghi nhớ bảy hằng đẳng thức (hawngf ddawngr thuwcs) đáng nhớ lớp 9 hiệu quả nhất mà Mas.edu.vn dành cho bạn:
Luyện tập thường xuyên
Học đi đôi với hành. Việc luyện tập thường xuyên sẽ giúp bạn ghi nhớ và vận dụng nhuần nhuyễn hơn bảy hằng đẳng thức (hawngf ddawngr thuwcs).
Bạn có thể thiết kế các bài tập ở nhiều dạng như điền vào chỗ chấm, cho sẵn một vế, viết vế còn lại.
Viết vào giấy note
Bạn có thể viết 7 hằng đẳng thức vào những tờ giấy ghi nhớ nhỏ, nhiều màu sắc như cách học từ vựng Tiếng Anh rồi dán lên góc học tập.
Học bài qua bài hát
Đọc bằng lời những hằng đẳng thức có thể khó nhớ nhưng đưa chúng vào trong bài hát thì việc ghi nhớ sẽ dễ dàng hơn.
Hiện nay có bài chế “Sau tất cả” với nội dung là 7 hằng đẳng thức. Giai điệu dễ nghe này đã thu hút sự chú ý của rất nhiều bạn trẻ.
Nhờ đó việc ghi nhớ bảy hằng đẳng thức không còn khô khan mà trở nên thuận lợi hơn.

Bài tập về 7 hằng đẳng thức đáng nhớ
Để củng cố nội dung 7 hằng đẳng thức đáng nhớ (hawngf ddawngr thuwcs), chúng ta cùng giải những bài tập trong SGK Toán nhé.
Câu hỏi trang 9 SGK Toán 8 tập 1
Với a và b là hai số bất kỳ, thực hiện phép tính (a + b) * (a + b).
Hướng dẫn giải
(a + b) * (a + b) = a * (a + b) + b * (a + b)
= a2 + a * b + b * a + b2
= a2 + 2 * a * b + b2
Câu hỏi trang 10 SGK Toán 8 tập 1
Tính [a + (-b)]2 (với a, b là các số tùy ý).
Hướng dẫn giải
Áp dụng hằng đẳng thức bình phương của một tổng ta có:
[a + (-b)]2 = a2 + 2 * a * (-b) + (-b)2 = a2 – 2 * a * b + b2
Câu hỏi trang 11 SGK Toán 8 tập 1
Ai đúng, ai sai ?
a2 – 10a + 25 = (a – 5)2
Thọ viết:
a2 – 10 * a + 25 = (5 – a)2.
Hương nêu nhận xét: Thọ viết sai, Đức viết đúng.
Sơn nói: Qua ví dụ trên mình rút ra được một hằng đẳng thức rất đẹp!
Hãy nêu ý kiến của em. Sơn rút ra được hằng đẳng thức nào ?
Hướng dẫn giải
Đức và Thọ đều viết đúng;
Hương nhận xét sai;
Sơn rút ra được hằng đẳng thức là: (a – 5)2 = (5 – a)2
Bài tập 16 trang 11 SGK Toán 8 tập 1
Viết các biểu thức sau đây dưới dạng bình phương của một tổng hoặc một hiệu:
a) a2 + 2a + 1
b) 9a2 + b2 + 6ab
c) 25a2 + 4b2 – 20ab
d) a2 – a + 1/4
Hướng dẫn giải
a) Áp dụng hằng đẳng thức (hawngf ddawngr thuwcs) bình phương của một tổng với A = a và B = 1
a2 + 2a + 1
= a2 + 2a1 + (1)2
= (a + 1)2
b) Áp dụng hằng đẳng thức (hawngf ddawngr thuwcs) bình phương của một tổng với A = 3a và B = b
9a2 + b2 + 6ab
= 9a2 + 6ab + b2
= (3a)2 + 2.3ab + b2
= (3a + b)2
c) Áp dụng hằng đẳng thức (hawngf ddawngr thuwcs) bình phương của một hiệu với A = 5a và B = 2b
25a2 + 4b2 – 20ab
= 25a2 – 20ab + 4b2
= (5a)2 – 2 * 5a * 2b + (2b)2
= (5a – 2b)2
d) Áp dụng hằng đẳng thức (hawngf ddawngr thuwcs) bình phương của một hiệu với với A = a và B = 1/2
a2 – a + 1/4
= a2 – 2 * a * 1/2 + (1/2)2
= (a – 1/2)2

Với những chia sẻ vừa rồi của Mas.edu.vn, hy vọng bạn đã nắm rõ 7 hằng đẳng thức (hawngf ddawngr thuwcs) đáng nhớ. Đừng quên theo dõi Mas.edu.vn để không bỏ qua những kiến thức thú vị.
Trong bài viết này, chúng ta đã tìm hiểu về 7 hằng đẳng thức đáng nhớ trong học đường. Chúng là những công thức quan trọng và được sử dụng rộng rãi trong các bài toán và bài tập toán học.
Qua việc áp dụng những hằng đẳng thức này, chúng ta có thể giải quyết các bài tập phức tạp một cách hiệu quả và nhanh chóng. Ngoài ra, việc nắm vững những hằng đẳng thức này cũng giúp chúng ta hiểu rõ hơn về các khái niệm và quy tắc trong toán học.
Hằng đẳng thức về tổ hợp, như công thức Newton và công thức Catalan, giúp chúng ta tính toán các tỷ lệ tổ hợp và xác suất một cách chính xác. Nhờ đó, ta có thể áp dụng chúng vào nhiều bài toán thực tế, từ quản lý dự án đến phân tích dữ liệu.
Hằng đẳng thức về chuỗi số, như công thức Gauss và công thức tổng trung bình của dãy số số học, rất hữu ích trong việc tính toán tổng các số hạng trong các dãy số cấp số cộng. Điều này giúp chúng ta tính toán các giá trị trung bình, dự đoán xu hướng và phân tích chuỗi dữ liệu.
Hằng đẳng thức về hàm lượng giác, như công thức sin, cos và tan của một góc, là các công thức quan trọng trong tính toán góc và các bài toán liên quan đến tam giác. Chúng giúp ta tính toán các giá trị của các hàm lượng giác trong các bài toán về hình học và vật lý.
Trên all, việc nắm vững và áp dụng thành thạo các hằng đẳng thức này không chỉ là một yêu cầu trong môi trường học tập mà còn là một kỹ năng quan trọng trong cuộc sống hàng ngày. Vì vậy, chúng ta nên dành thời gian học tập và luyện tập để hiểu rõ và sử dụng linh hoạt những công thức này.
Cảm ơn bạn đã xem bài viết Hawngf ddawngr thuwcs – Bài tập về 7 hằng đẳng thức đáng nhớ tại Mas.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Định nghĩa của hàm đáng nhớ
2. Công thức hàm đáng nhớ
3. Công thức tổng của hằng đẳng thức đáng nhớ
4. Sự áp dụng của hằng đẳng thức đáng nhớ trong toán học
5. Một số ví dụ về hằng đẳng thức đáng nhớ
6. Cách chứng minh hằng đẳng thức đáng nhớ
7. Tính chất của hằng đẳng thức đáng nhớ
8. Mối quan hệ giữa hằng đẳng thức đáng nhớ và các phép toán khác
9. Ứng dụng của hằng đẳng thức đáng nhớ trong vật lý và kỹ thuật
10. Hằng đẳng thức đáng nhớ và cải tiến kỹ thuật tính toán
11. Sự khác biệt giữa hằng đẳng thức đáng nhớ và hàm tuyến tính
12. Công dụng của hằng đẳng thức đáng nhớ trong giải tích
13. Định lý hằng đẳng thức đáng nhớ và các định lý tương tự
14. Hằng đẳng thức đáng nhớ trong việc giải các bài toán toán học khó
15. Tầm quan trọng của hằng đẳng thức đáng nhớ trong nghiên cứu khoa học.