Bạn đang xem bài viết Phương trình vô nghiệm khi nào? Bài tập tìm m để phương trình vô nghiệm tại Mas.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Phương trình vô nghiệm là một khái niệm quan trọng trong học phương trình. Để hiểu rõ hơn về phương trình vô nghiệm và các bài tập liên quan, chúng ta cần đi vào khám phá sự tương quan giữa các hệ số và biến số trong phương trình. Trong bài viết này, chúng ta sẽ tìm hiểu về một dạng bài tập đặc biệt, đó là tìm giá trị của m để phương trình trở thành vô nghiệm. Chắc hẳn sau khi đọc xong bài viết này, bạn sẽ nắm vững cách tiến hành và giải quyết những bài tập tương tự.
Phương trình vô nghiệm khi nào? Một trong những bài toán các bạn học sinh vẫn thường gặp là “tìm m để phương trình vô nghiệm”. Bài viết này của Mas.edu.vn sẽ tổng hợp kiến thức về phương trình vô nghiệm, đưa ra những dạng toán thường gặp về phương trình vô nghiệm và cách giải chi tiết nhất. Hy vọng giúp các bạn học sinh rèn luyện thêm kiến thức để chuẩn bị cho các kì thi thật tốt. Cùng khám phá ngay thôi nào!
Danh Mục Bài Viết
Phương trình vô nghiệm là gì?
Phương trình vô nghiệm là phương trình không có nghiệm nào. Phương trình vô nghiệm có tập nghiệm là S = Ø
Một phương trình có thể có một nghiệm, hai nghiệm, ba nghiệm,… nhưng cũng có thể không có nghiệm nào hoặc vô số nghiệm.
Phương trình vô nghiệm khi nào? Điều kiện để phương trình vô nghiệm
Phương trình vô nghiệm khi nào?
Bất phương trình vô nghiệm <=> a=0 và b xét với dấu > thì b ≤0≤0; với dấu < thì b ≥0.
Điều kiện để phương trình vô nghiệm là gì?
Phương trình bậc nhất một ẩn:
Phương trình bậc nhất một ẩn ax + b = 0 vô nghiệm khi a = 0, b ≠ 0
Phương trình bậc hai một ẩn:
Phương trình bậc hai một ẩn ax + bx + c = 0 vô nghiệm khi a ≠ 0, ∆ < 0
Công thức phương trình vô nghiệm
Phương trình bậc nhất một ẩn:
Xét phương trình bậc nhất có dạng ax + b = 0.
Nếu a = 0, b ≠ 0 thì phương trình vô nghiệm.
Phương trình bậc hai một ẩn:
Xét phương trình bậc hai có dạng ax^2 + bx + c = 0 (a ≠ 0).
- Công thức nghiệm tính delta (ký hiệu là ∆).
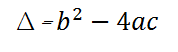
Nếu ∆ < 0 thì phương trình vô nghiệm.
- Công thức nghiệm thu gọn tính ∆’ (chỉ tính ∆’ khi hệ số b chẵn).
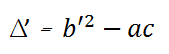
Với b = 2b’
Nếu ∆’ < 0 thì phương trình vô nghiệm.
Một số bài mẫu tìm m để phương trình vô nghiệm
Dưới đây là những bài toán tham khảo về dạng toán “tìm m để phương trình vô nghiệm”
Bài 1: Tìm m để phương trình sau vô nghiệm:
![]()
Hướng dẫn:
Do hệ số ở biến x2 là một số khác 0 nên phương trình là phương trình bậc hai một ẩn.
Ta sẽ áp dụng điều kiện để phương trình bậc hai một ẩn vô nghiệm vào giải bài toán.
Để phương trình 5x^2 – 2x + m = 0 vô nghiệm thì ∆’ < 0
⇔ 4 – 5m < 0
⇔ m > ⅘
Vậy với m > ⅘ thì phương trình 5x^2 – 2x + m = 0 vô nghiệm

Bài 2: Tìm m để phương trình sau vô nghiệm:
![]()
Hướng dẫn:
Do hệ số ở biến x2 có chứa tham số m, nên khi giải bài toán ta phải chia hai trường hợp là m = 0 và m ≠0.
Lời giải: Bài toán được chia thành 2 trường hợp:
TH1: m = 0
Phương trình trở thành phương trình bậc nhất một ẩn 2x + 1 = 0 ⇔ x = -½ (loại)
Với m = 0 thì phương trình mx^2 – 2(m – 1)x + m + 1 = 0 có nghiệm x = -½
TH2: m ≠ 0
Phương trình trở thành phương trình bậc hai một ẩn: mx^2 – 2(m – 1)x + m + 1 = 0
Để phương trình vô nghiệm thì ∆’ < 0
⇔ (m – 1)^2 – m.(m + 1) < 0
⇔ m^2 – 2m + 1 – m^2 – m < 0
⇔ -3m < -1
⇔ m > ⅓
Vậy với m > ⅓ thì phương trình mx^2 – 2(m – 1)x + m + 1 = 0 vô nghiệm

Bài 3: Tìm m để phương trình sau vô nghiệm:
![]()
Hướng dẫn:
Do hệ số ở biến x2 là một số khác 0 nên phương trình là phương trình bậc hai một ẩn. Ta sẽ áp dụng điều kiện để phương trình bậc hai một ẩn vô nghiệm vào giải bài toán.
Lời giải: Để phương trình 3×2 + mx + m2 = 0 vô nghiệm thì ∆ < 0
⇔ m^2 – 4.3.m^3 < 0
⇔ -11m^2 < 0∀m ≠ 0
Vậy với mọi m ≠ 0 thì phương trình 3×2 + mx + m2 = 0 vô nghiệm.
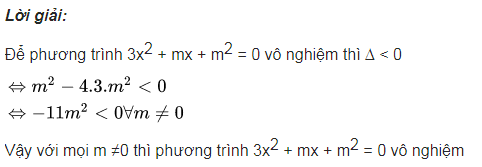
Bài 4: Tìm m để phương trình sau vô nghiệm
![]()
Hướng dẫn:
Do hệ số ở biến x2 có chứa tham số m, nên khi giải bài toán ta phải chia hai trường hợp là m = 0 và m ≠0.
Lời giải:
- TH1: m = 0
Phương trình trở thành phương trình bậc nhất một ẩn 0x = -3 (phương trình vô nghiệm)
Với m = 0 thì phương trình vô nghiệm
- TH2: m ≠ 0
Để phương trình m2x2 – 2m2x + 4m2 + 6m + 3 = 0 vô nghiệm thì ∆’ < 0
⇔ (-m^2)^2 – m^2 (4m^2 + 6m + 3) < 0
⇔ -3m^4 – 6m^3 – 3m^2 < 0
⇔ -3m^2 .(m^2 + 2m +1) < 0
⇔ -3m^2 .(m+1)^2 < 0∀m ≠ m-1
Vậy với mọi m ≠ – 1 thì phương trình m2x2 – 2m2x + 4m2 + 6m + 3 = 0 vô nghiệm

Như vậy bài viết trên đã giải đáp được thắc mắc Phương trình vô nghiệm khi nào? Đồng thời với những bài tập mẫu mà Mas.edu.vn chia sẻ, hy vọng sẽ giúp các bạn nắm vững kiến thức và rèn luyện tốt hơn. Chúc các bạn học tập tốt!
Trong toán học, một phương trình được gọi là vô nghiệm khi không tồn tại giá trị của biến mà khi thay vào phương trình, phương trình không thỏa mãn. Điều này có nghĩa là tập hợp các giá trị của biến không chứa bất kỳ giá trị nào để phương trình trở thành một câu lệnh đúng.
Để tìm phương trình vô nghiệm, chúng ta cần xem xét cách các thành phần của phương trình tương tác với nhau. Có một số trường hợp khi phương trình trở thành vô nghiệm. Dưới đây là một số ví dụ:
1. Phương trình bậc nhất: Phương trình dạng ax + b = 0, trong đó a và b là các hằng số. Để phương trình này không có nghiệm, hệ số a phải bằng 0 và hệ số b khác 0.
2. Phương trình bậc hai: Phương trình dạng ax^2 + bx + c = 0, trong đó a, b và c là các hằng số. Để phương trình này không có nghiệm, ta có thể sử dụng công thức delta để kiểm tra giá trị của biểu thức delta = b^2 – 4ac. Nếu delta
Cảm ơn bạn đã xem bài viết Phương trình vô nghiệm khi nào? Bài tập tìm m để phương trình vô nghiệm tại Mas.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Vô nghiệm
2. Không có nghiệm
3. Phương trình không có giá trị
4. Phương trình không có nghiệm x
5. Bài toán tìm m để phương trình vô nghiệm
6. Điều kiện để phương trình không có nghiệm
7. Giá trị m để phương trình vô nghiệm
8. Tìm m để phương trình ax^2 + bx + c = 0 vô nghiệm
9. Phương trình bậc hai vô nghiệm
10. Điều kiện để phương trình bậc hai không có nghiệm
11. Công thức tính giá trị m để phương trình vô nghiệm
12. Mệnh đề phương trình vô nghiệm
13. Giải bài toán tìm m để phương trình vô nghiệm
14. Tìm điều kiện vô nghiệm cho phương trình
15. Phương trình ax^2 + bx + c không có nghiệm