Số thực là gì? Tính chất của số thực

Toán học là một trong những bộ môn bắt buộc mà chúng ta được học từ bé đến lớn. Toán học có rất nhiều ứng dụng trong cuộc sống. Một trong đó là số thực. Vậy số thực là gì? Cùng Mas.edu.vn tìm hiểu trong bài viết sau đây!

Số thực là gì?

Số thực là gì?

Số thực là tập hợp số bao gồm các số dương (1, 2, 3,…), số 0, số âm (-1, -2, -3,…), số hữu tỉ (5/2, -2/3), số vô tỉ (số pi, số √2). Số thực có thể được xem là các điểm nằm trên trục số dài vô hạn.

Tập hợp số thực được kí hiệu là R. Số thực chính là tập hợp các số hữu tỉ và vô tỉ: R = Q ∪ I.

Ngoài ra, một số thực có thể là số đại số hoặc số siêu việt. Số thực bao gồm số thực âm và số thực dương.

Như vậy, số thực bao gồm:

• Số tự nhiên N: N = {0, 1, 2, 3,…}
• Số nguyên Z: Z = {…, -3, -2, -1, 0, 1, 2, 3,…}
• Số hữu tỉ Q: Q = {x = a/b; trong đó a,b ϵ Z, và b ≠0}
• Số vô tỉ I: I ={số thập phân vô hạn không tuần hoàn, ví dụ √2, số pi}

Ví dụ số thực là gì?

Các ví dụ về số thực là:

• Số tự nhiên như: 1, 2, 3, 4, 5,…
• Số nguyên như: −15, -2, 3, 8,…
• Số hữu tỉ như: 4/3, 8/10,…
• Số vô tỉ như: √2 (1,41421356…); 3,1456…,….

Trục số thực là gì?

Trục số thực là một trục số nằm ngang để biểu diễn tập hợp các số thực. Mỗi số thực được biểu diễn bởi một điểm trên trục số.

Ngược lại, mỗi điểm trên trục số sẽ biểu diễn một số thực. Chỉ có tập hợp số thực mới có thể lấp đầy trục số.

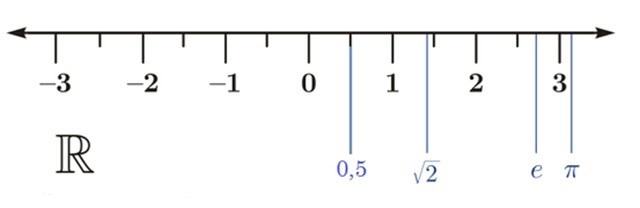
Trong tập hợp R, ta cũng định nghĩa các phép toán cộng trừ, nhân, chia, lũy thừa, căn bậc,…Và trong các phép toán, các số thực cũng có các tính chất như các phép toán trong tập hợp các số hữu tỉ.

Tính chất của số thực là gì?

Các tính chất của số thực:

• Bất kỳ số thực nào khác 0 thì sẽ là số âm hoặc số dương.
• Tổng hay tích của hai số thực không âm là một số thực không âm.
• Số thực là tập hợp vô hạn các số vô cùng nhiều không đếm được các số thực.
• Số thực có hệ thống các tập hợp con vô hạn có thể đếm được.
• Số thực có thể biểu thị bằng biểu diễn thập phân.
• Số thực có thể được sử dụng để thể hiện các phép đo đại lượng liên tục.

Các thuộc tính của số thực là gì?

Số thực có hai thuộc tính cơ bản là thuộc tính trường có thứ tự và thuộc tính cận trên thấp nhất.

Thuộc tính trường có thứ tự

Thuộc tính này chỉ rằng các số thực bao gồm một trường, với phép cộng và phép nhân cùng với phép chia cho các số khác không. Chúng có thể được sắp xếp hoàn toàn trên một trục số hoành theo cách tương thích với phép cộng và phép nhân.

Thuộc tính cận trên thấp nhất

Thuộc tính này chỉ ra rằng nếu tập hợp một số thực không trống có giới hạn trên thì nó có cận trên chính là những số thực nhỏ nhất.

Tập hợp của số thực là gì?

Tập hợp R là ký hiệu của tập hợp số thực, bao gồm các số thực. Số thực gồm có số hữu tỉ và số vô tỉ.

• Số hữu tỉ là số được viết dưới dạng phân số phân số a/b (a,b ∈ Z, b ≠ 0). Tập hợp số hữu tỉ ký hiệu là Q.

Ví dụ: −1/5; 2/3,….

• Số vô tỉ là số thập phân vô hạn không tuần hoàn. Tập hợp số vô tỉ được ký hiệu là I.

Ví dụ: √2; 3,1415…

Ta có: N ⊂ Z ⊂ Q, cho nên R = Q ∪ I.

Tập số thực R phủ kín trục số.

Sự khác nhau giữa số nguyên và số thực là gì?

Số nguyên là gì?

Số nguyên là tập hợp số bao gồm các số 0, số tự nhiên dương và số tự nhiên âm. Tập hợp số nguyên tuy là vô hạn nhưng có thể đếm được.

Số nguyên được chia làm hai loại là số nguyên dương và số nguyên âm. Kí hiệu của tập số nguyên là Z.

Sự khác nhau giữa số nguyên và số thực là gì?

Sự khác nhau giữa số nguyên và số thực là:

• Số thực là tập hợp các số không đếm được.
• Số nguyên là tập hợp các số đếm được.
• Ngoài ra, số nguyên là một trong các tập con của số thực.

Các dạng bài tập toán thường gặp liên quan đến số thực là gì?

Dạng 1: Các câu hỏi về bài tập hợp số

Phương pháp sử dụng: Sử dụng các ký hiệu về tập hợp số. Trong đó:

• N: Tập hợp các số tự nhiên
• Z: Tập hợp các số nguyên
• Q: Tập hợp các số hữu tỉ
• I: là tập hợp các số vô tỉ
• R: là tập hợp các số thực

Ta có quan hệ giữa các tập hợp số như sau: N ⊂ Z ⊂ Q ⊂ R; I ⊂ R.

Dạng 2: Tìm số chưa biết trong một đẳng thức

Phương pháp sử dụng:

• Sử dụng từ tính chất của các phép toán.
• Sử dụng quan hệ giữa các số hạng trong một tổng và một hiệu; quan hệ giữa các thừa số trong một tích; quan hệ giữa số bị chia, số chia và thương trong phép chia.
• Sử dụng quy tắc chuyển vế, phá dấu ngoặc.

Dạng 3: Tính giá trị của biểu thức nào đó

Phương pháp sử dụng:

• Thực hiện các phép tính cộng, trừ, nhân, chia và lũy thừa. Cần lưu ý đến thứ tự thực hiện: nhân chia trước, cộng trừ sau.
• Rút gọn các phân số khi cần.
• Vận dụng các tính chất của phép toán sao cho thích hợp.

Qua bài viết trên, Mas.edu.vn đã giúp bạn biết được khái niệm số thực là gì và cách kí hiệu của số thực. Giờ đây, chúng ta có thể áp dụng ngay kiến thức để giải các bài toán thôi nào.