Bạn đang xem bài viết Tính chất hình bình hành là gì? 7 bài tập liên quan tại Mas.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Hình bình hành, còn được gọi là hình tứ diện đều, là một khái niệm quan trọng trong hình học không gian. Với những tính chất đặc biệt của mình, hình bình hành đã thu hút sự quan tâm của các nhà toán học và được áp dụng rộng rãi trong nhiều lĩnh vực, từ công nghệ và kiến trúc đến thiết kế và khoa học tự nhiên.
Tính chất cơ bản của hình bình hành là nó có 4 cạnh và 4 đỉnh, với các cạnh song song và đôi mặt song song nhau. Điều này mang lại cho nó những đặc điểm riêng biệt và dễ nhận biết. Đồng thời, hình bình hành cũng có các đường chéo đối xứng, tạo nên một cấu trúc cân đối và hài hòa.
Để hiểu rõ hơn về tính chất của hình bình hành, chúng ta có thể tìm hiểu qua 7 bài tập liên quan. Những bài tập này sẽ giúp ta khám phá thêm về các định nghĩa, công thức và quy luật liên quan đến hình bình hành. Bên cạnh đó, chúng cũng sẽ giúp ta nắm vững cách tính diện tích và chu vi của hình bình hành, cũng như các mối liên hệ và ứng dụng của chúng trong thực tế.
Bằng việc tìm hiểu và giải quyết các bài tập liên quan đến hình bình hành, chúng ta sẽ có cơ hội rèn luyện kỹ năng tư duy logic, sự linh hoạt trong suy nghĩ và khả năng áp dụng kiến thức toán học vào thực tế. Hơn nữa, việc nắm vững về tính chất của hình bình hành sẽ giúp ta đạt được sự hiểu biết sâu sắc và mở ra những cánh cửa mới trong lĩnh vực này.
Vậy, hãy bắt đầu hành trình khám phá tính chất hình bình hành qua 7 bài tập liên quan để thấy được sự đa dạng và thú vị của tư duy toán học và ứng dụng của nó trong cuộc sống hàng ngày.
Hình học trong lĩnh vực Toán học là bộ môn quan trọng trong chương trình dạy học. Trong đó, phải kể đến là hình bình hành. Vậy đâu là tính chất hình bình hành? Những bài toán liên quan đến tính chất hình bình hành sẽ được giải đáp như thế nào? Tất cả sẽ được Mas.edu.vn trình bày ngay sau đây.
Danh Mục Bài Viết
Hình bình hành là gì?
Hình bình hành là gì?
Hình bình hành trong hình học là một hình tứ giác được tạo thành khi hai cặp đường thẳng song song cắt nhau. Nói đơn giản, hình bình hành là tứ giác có các cạnh đối song song.
Nó là một dạng đặc biệt của hình thang. Trong không gian ba chiều, khối tương đương với hình bình hành là hình khối lục diện.
Dấu hiệu nhận biết hình bình hành
Các dấu hiệu nhận biết hình bình hành là:
Nếu hình bình hành là một tứ giác đặc biệt:
- Tứ giác có hai cặp cạnh đối song song là hình bình hành.
- Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành.
- Tứ giác có một cặp cạnh đối vừa song song và vừa bằng nhau là hình bình hành.
- Tứ giác có các góc đối bằng nhau là hình bình hành.
- Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Nếu hình bình hành là hình thang:
- Hình thang có hai cạnh đáy bằng nhau là hình bình hành.
- Hình thang có hai cạnh bên song song là hình bình hành
Tính chất hình bình hành
Các tính chất hình bình hành:
Tính chất 1: Trong hình bình hành, các cạnh đối song song và bằng nhau.
Trong hình bình hành ABCD có các cạnh đối song song bằng nhau là AB và CD, AD và BC.
Tính chất 2: Trong hình bình hành, các góc đối bằng nhau.
Trong hình bình hành ABCD có các góc đối bằng nhau là góc A và góc C, góc B và góc D.
Tính chất 3: Trong hình bình hành, hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Hình bình hành ABCD có AC cắt BD tại O. Suy ra, các đường thẳng OA và OC bằng nhau, OB và OD bằng nhau.
Một số công thức liên quan đến hình bình hành
Công thức tính chu vi hình bình hành
Chu vi hình bình hành bằng tổng độ dài bốn cạnh của hình bình hành. Hay nói cách khác, chu vi hình bình hành bằng hai lần tổng một cặp cạnh kề nhau bất kỳ.
Công thức tính chu vi hình bình hành: P = (a + b) x 2
Trong đó: P là chu vi; a, b là độ dài hai cạnh bất kỳ.
Ví dụ: Cho hình bình hành ABCD có hai cạnh a và b lần lượt là 4cm và 5cm. Hỏi chu vi của hình bình hành ABCD là bao nhiêu?
Cách giải: Áp dụng công thức, ta có: P = (4 + 5) x 2 = 18 (cm). Vậy chu vi hình bình hành ABCD là 18 cm.
Công thức tính diện tích hình bình hành
Diện tích hình bình hành bằng tích của chiều cao với cạnh đáy tương ứng.
Công thức tính diện tích hình bình hành: S = a.h
Trong đó: S là diện tích hình bình hành; h là chiều cao của hình bình hành và a là độ dài cạnh đáy tương ứng.
Ví dụ: Cho hình bình hành ABCD có cạnh đáy CD = 8cm, chiều cao nối từ đỉnh A xuống cạnh CD dài 6cm. Hỏi diện tích của hình bình hành ABCD là bao nhiêu?
Cách giải: Áp dụng công thức, ta có: S = 8.6 = 48 (cm²). Vậy diện tích hình bình hành ABCD là 48 cm².
Bài tập về cách chứng minh tính chất hình bình hành
Bài tập 1
Các câu sau đúng hay sai?
a) Hình thang có hai cạnh đáy bằng nhau là hình bình hành.
b) Hình thang có hai cạnh bên song song là hình bình hành.
c) Tứ giác có hai cạnh đối bằng nhau là hình bình hành.
d) Hình thang có hai cạnh bên bằng nhau là hình bình hành.
Lời giải:
a) Đúng, vì hình thang có hai đáy song song với có thêm hai cạnh đáy bằng nhau thì sẽ là hình bình hành theo dấu hiệu nhận biết.
b) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa).
c) Sai, vì tứ giác có hai cạnh đối (hai cạnh bên) bằng nhau nhưng không song song nên nó không phải là hình bình hành.
d) Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng không song song nên nó không phải là hình bình hành (theo tính chất hình bình hành).
Bài tập 2
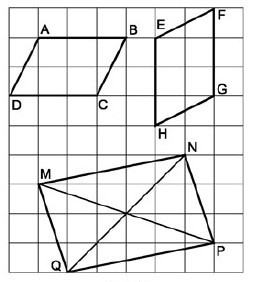
Các tứ giác ABCD, EFGH, MNPQ trên giấy kẻ ô vuông như hình bên dưới có phải là hình bình hành hay không?
Lời giải:
Cả ba tứ giác trên đề là hình bình hành vì:
- Tứ giác ABCD có AB // CD và AB = CD = 3 ⇒ tứ giác này là hình bình hành (dấu hiệu nhận biết)
- Tứ giác EFGH có EH // FG và EH = FH = 3 ⇒ tứ giác này là hình bình hành (dấu hiệu nhận biết)
- Tứ giác MNPQ có MN = PQ và MQ = NP ⇒ tứ giác này là hình bình hành (dấu hiệu nhận biết)
Bài tập 3
Cho hình bình hành ABCD. Gọi E, F là trung điểm của AD, BC. Chứng minh rằng BE = DF
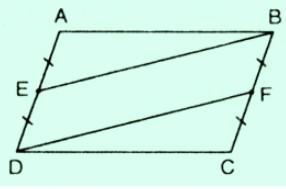
Lời giải:
Ta có: DE = 1/2.AD; BF = 1/2.BC
ABCD là hình bình hành ⇒ AD = BF
=> DE = BF
Tứ giác BEDF có: DE // BF (vì AD // BC) và DE = BF
⇒ BEDF là hình bình hành
⇒ BE = DF
Bài tập 4
Cho hình bình hành ABCD (AB>BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.
a) Chứng minh rằng DE // BF
b) Tứ giác DEBF là hình gì? Vì sao?
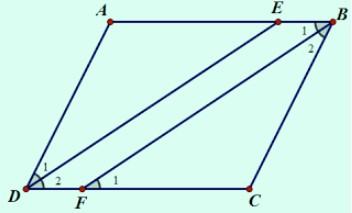
Lời giải:

b) Tứ giác DEBF có:
DE // BF (chứng minh ở câu a)
BE // DF (vì AB // CD)
⇒ Tứ giác DEBF là hình bình hành.
Bài tập 5
Cho hình hình bình hành ABCD. AH, CH cùng vuông góc với BD.
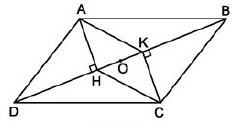
a) Chứng minh rằng AHCK là hình bình hành.
b) Gọi O là trung điểm của HK. Chứng minh rằng ba điểm A, O, C thẳng hàng.
Lời giải:
a) Hai tam giác vuông AHD và CKB có:
AD = CB (giả thiết)
∠D1 = ∠B1 (so le trong)
⇒ ∆AHD = ∆CKB (cạnh huyền, góc nhọn)
⇒ AH = CK
Tứ giác AHCK có AH // CK, AH = CK. Theo tính chất hình bình hành, suy ra AHCK là hình bình hành.
b) Xét hình bình hành AHCK, O là trung điểm của đường chéo hình bình hành. Do đó, ba điểm A, O, C thẳng hàng.
Bài tập 6
Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?
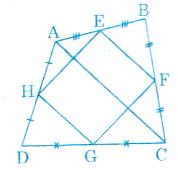
Lời giải:
Tứ giác EFGH là hình bình hành.
Cách 1: EB = EA, FB = FC (giả thiết)
Cho nên, EF là đường trung bình của ∆ABC. Do đó, EF // AC
Tương tự, HG là đường trung bình của ∆ACD. Do đó, HG // AC
⇒ EF // HG (1)
Chứng minh tương tự ⇒ EH // FG (2)
Từ (1) và (2) suy ra EFGH là hình bình hành (dấu hiệu nhận biết).
Cách 2: EF là đường trung bình của ∆ABC nên EF = 1/2 AC
HG là đường trung bình của ∆ACD nên HG = 1/2 AC
Suy ra, EF = HG
Ta có: EF // HG ( chứng minh trên)
Vậy EFGH là hình bình hành (dấu hiệu nhận biết).
Bài tập 7
Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:
a) AI // CK
b) DM = MN = NB
Lời giải:
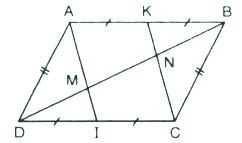
a) Tứ giác ABCD có AB = CD, AD = BC nên là hình bình hành.
Tứ giác AICK có AK // IC, AK = IC nên AICK là hình bình hành.
Do đó, AI // CK
b) ∆DCN có DI = IC, IM // CN
Vì AI // CK nên suy ra DM = MN
Chứng minh tương tự đối với ∆ABM ta có MN = NB.
Vậy DM = MN = NB
Trên đây là những tính chất hình bình hành và các bài tập về cách chứng minh hình bình hành mà Mas.edu.vn muốn chia sẻ đến các bạn. Chúc các bạn độc giả sẽ có thêm những kiến thức Toán học thú vị và hay ho. Nhớ Like và Share bài viết của chúng tôi nhé!
Tính chất hình bình hành là một khái niệm cơ bản trong hình học, được sử dụng để mô tả các đặc điểm và quan hệ giữa các phần tử của hình bình hành. Đây là một chủ đề quan trọng trong giáo dục toán học và được áp dụng trong nhiều lĩnh vực khác nhau trong đời sống hàng ngày.
Có một số tính chất cơ bản của hình bình hành mà chúng ta cần nắm vững. Đầu tiên là các cạnh đối xứng: một hình bình hành có cặp cạnh song song và bằng nhau; điều này đồng nghĩa với việc góc giữa các cặp cạnh là bằng nhau. Thứ hai, các đường chéo của hình bình hành chia nhỏ nó thành hai tam giác đồng dạng và bằng nhau. Đặc biệt, đường chéo chính cắt nhau ở một điểm giữa, nằm giữa các đỉnh của hình. Thứ ba, hình bình hành có hai cặp đường chéo đối xứng; điều này có nghĩa là đường chéo từ hai cặp đỉnh đối diện là bằng nhau và cắt nhau ở một góc vuông.
Để nắm vững tính chất này, chúng ta cần thực hành qua các bài tập. Dưới đây là 7 bài tập liên quan đến tính chất hình bình hành:
1. Xác định tất cả các cạnh đối xứng của một hình bình hành cho trước.
2. Tìm đường chéo chính của một hình bình hành và tính toán chiều dài của nó.
3. Cho một hình bình hành với đường chéo chính đã biết, tìm độ dài cạnh của nó.
4. Xác định các đường chéo của một hình bình hành và tính toán diện tích của hai tam giác đồng dạng tạo thành từ đường chéo đó.
5. Tìm góc giữa các cặp cạnh đối xứng trong một hình bình hành.
6. Xác định điểm giao của hai đường chéo của một hình bình hành và tính toán khoảng cách từ điểm giao đó đến mỗi đỉnh.
7. Tìm xem có tồn tại các điểm nằm ở bên trong hình bình hành nhưng không thuộc vào các cạnh hoặc đường chéo của nó.
Trên đây chỉ là một số bài tập cơ bản để nắm vững tính chất hình bình hành. Bằng cách thực hiện những bài tập này, chúng ta có thể nâng cao kiến thức và hiểu biết về tính chất cũng như ứng dụng của hình bình hành trong thực tế.
Cảm ơn bạn đã xem bài viết Tính chất hình bình hành là gì? 7 bài tập liên quan tại Mas.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Hình bình hành
2. Các đường chéo của hình bình hành
3. Các đỉnh và cạnh của hình bình hành
4. Đường chéo chia đôi góc của hình bình hành
5. Diện tích hình bình hành
6. Chu vi hình bình hành
7. Công thức tính diện tích hình bình hành
8. Công thức tính chu vi hình bình hành
9. Hình bình hành đặc biệt: hình vuông, hình chữ nhật
10. Đặc điểm của hình bình hành vuông góc
11. Các đặc điểm của hình bình hành cân
12. Các tính chất hình học của hình bình hành
13. Hình bình hành và hình thang
14. Tính chất hình bình hành và các đa giác khác
15. Bài tập về tính chất hình bình hành.