Bạn đang xem bài viết Tính chất hình thang vuông? 3 bài tập về hình thang vuông tại Mas.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Hình thang vuông là một dạng hình học đặc biệt, có những tính chất đặc trưng riêng biệt. Để hiểu rõ hơn về tính chất của hình thang vuông, chúng ta hãy cùng tìm hiểu qua ba bài tập sau đây.
Bài tập 1: Cho hình thang vuông ABCD có đáy AB và CD đồng quy và vuông góc với nhau. Gọi H là trung điểm của cạnh CD. Chứng minh rằng hai đường chéo AC và BD bằng nhau và vuông góc với nhau.
Bài tập 2: Trên các cạnh AB và CD của hình thang vuông ABCD, lần lượt lấy các điểm M và N sao cho AM = BN. Chứng minh rằng hai đường thẳng CM và DN cắt nhau tại một điểm E và AE vuông góc với BC.
Bài tập 3: Cho hình thang vuông ABCD có đáy AB và CD đồng quy. Kẻ đường cao AH và gọi M là trung điểm của cạnh AD. Chứng minh rằng đường thẳng BM đi qua trung điểm của đoạn thẳng CH.
Qua những bài tập trên, ta có thể thấy rằng hình thang vuông có những tính chất đặc biệt như: đường chéo vuông góc và bằng nhau, đường cao chia hai đường chéo thành hai phần bằng nhau, đường thẳng qua hai trung điểm của các cạnh tạo thành một đường thẳng song song với cạnh đáy. Từ đó, chúng ta có thể áp dụng các tính chất này để giải quyết những bài toán liên quan đến hình thang vuông.
Hình thang vuông được sử dụng trong bộ môn Toán hình học. Vậy liệu các bạn có còn nhớ tính chất hình thang vuông? Hãy cùng Mas.edu.vn ôn tập lại kiến thức này nhé!
Danh Mục Bài Viết
Định nghĩa hình thang vuông
Hình thang là gì?
Hình thang là một tứ giác lồi có hai cạnh đối song song. Hai cạnh song song này được gọi là hai cạnh đáy. Hai cạnh còn lại gọi là hai cạnh bên.
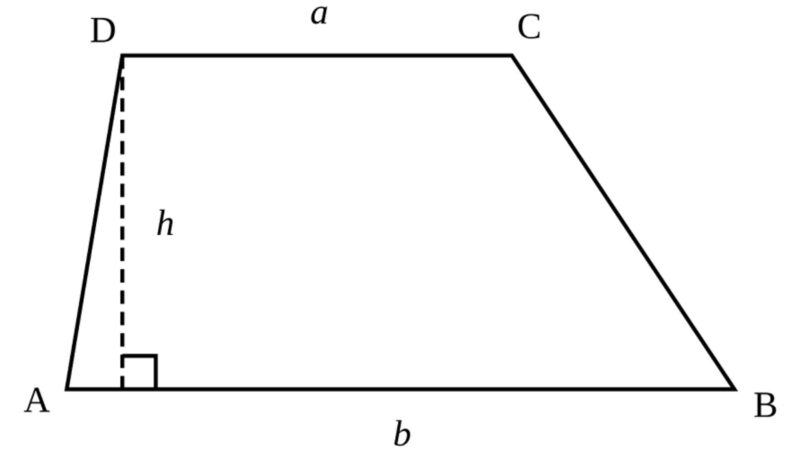
Các trường hợp đặc biệt của hình thang là:
- Hình thang vuông
- Hình thang cân
- Hình thang vuông cân hay còn được gọi là hình chữ nhật
Trong thực tế ta có thể dễ nhận thấy minh họa về hình thang nhất là hình cây thang hoặc những chiếc bàn có mặt bàn hình thang.
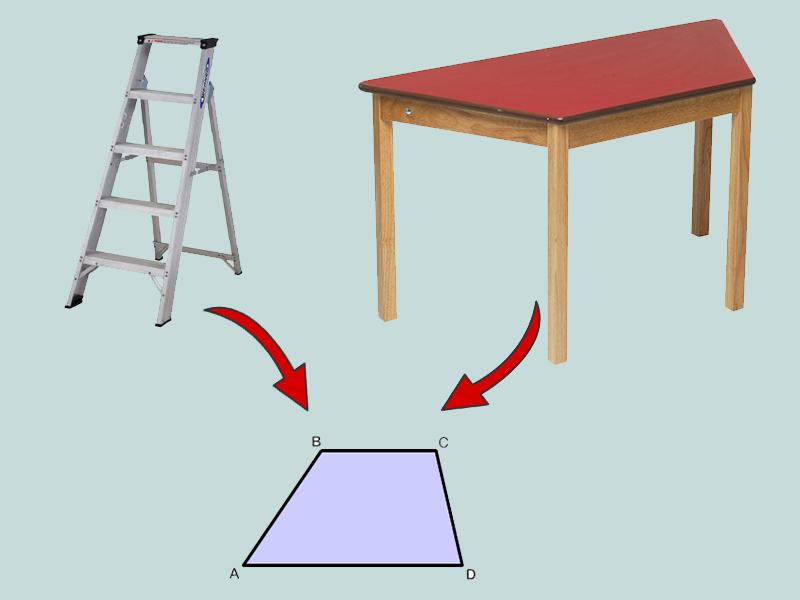
Hình thang vuông là gì?
Hình thang vuông là hình thang có một góc vuông (90°). Nói cách khác, hình thang vuông là một trường hợp đặc biệt của hình thang.
Tính chất hình thang vuông và dấu hiệu nhận biết hình thang vuông
Tính chất hình thang vuông
Hình thang vuông có hai cạnh đáy song song và vuông góc với hai đáy, tạo nên góc 90 độ.
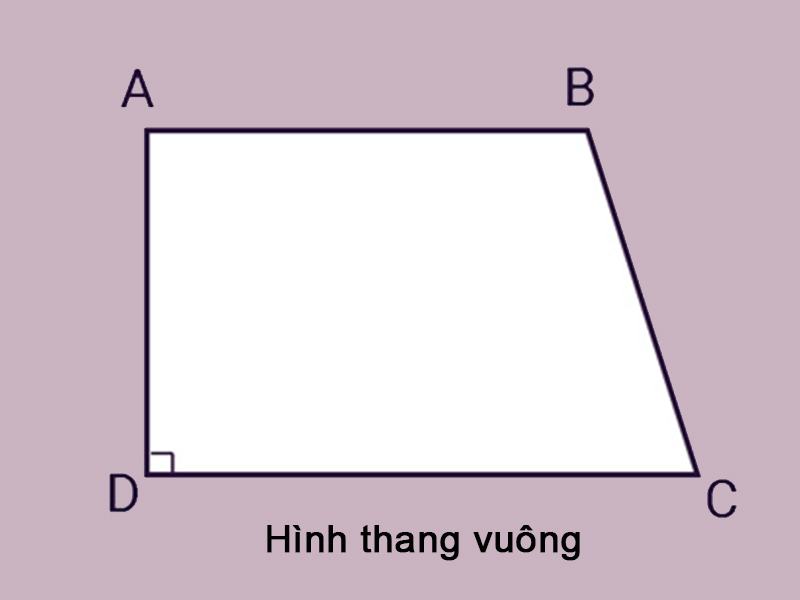
Dấu hiệu nhận biết hình thang vuông
Dấu hiệu để nhận biết hình thang vuông đó chính là hình thang có một góc vuông. Đáp ứng điều kiện này thì tứ giác là hình thang vuông.
Công thức liên quan đến tính chất hình thang vuông
Công thức tính diện tích hình thang vuông
Diện tích hình thang vuông bằng một nửa tích của tổng hai đáy và chiều cao ứng với cạnh đáy hoặc bằng tích của đường cao và trung bình cộng của hai đáy.
S = ½ h . (a + b)
Trong đó:
- a, b: Độ dài 2 đáy của hình thang
- h: Độ dài đường cao (chính là cạnh vuông góc với 2 cạnh đáy)
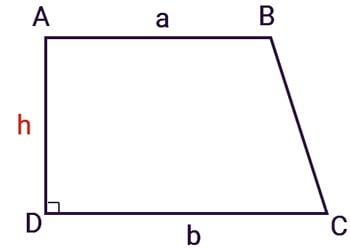
Công thức tính chu vi hình thang vuông
Chu vi hình thang vuông bằng tổng của hai cặp cạnh.
P = a + b + c + d
Trong đó: a, b, c, d là độ dài các cạnh đáy và các cạnh bên của hình thang vuông.
Chủ đề liên quan:
- Tính chất đường phân giác trong tam giác? Lý thuyết & bài tập
- Tính chất cơ bản của phân thức là gì? 3 Dạng toán cơ bản của phân thức
Các dạng bài tập liên quan đến tính chất hình thang vuông
Bài tập 1
Hình thang vuông ABCD (AB//CD) có AB = 3cm, CD = 6cm, và AD = 4cm. Tính diện tích hình thang ABCD.
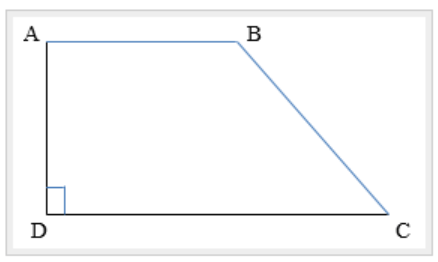
Lời giải:
Hình thang ABCD có AB // CD nên hai đáy là AB, CD
AD ⊥ DC
Suy ra, AD là chiều cao của hình thang.
Áp dụng công thức: S = ½ h . (a + b) = ½ . 4 . ( 3 + 6) = 18 (cm²)
Vậy diện tích của hình thang ABCD là 18cm².
Bài tập 2
Cho hình thang vuông ABCD có AD = 6cm; DC = 12cm; AB = 2/3 DC
a) Tính diện tích hình thang ABCD?
b) Khi kéo dài cạnh bên AD và CB thì 2 cạnh bên này cắt nhau tại M. Tính độ dài cạnh AM?
Lời giải:
a) Độ dài cạnh AB là:
AB = 2/3 DC = 12 . (2/3) = 8cm
Diện tích ABCD : (8 + 12) / 2 . 6 = 60cm
b) Xét tam giác ABC đáy AB và DBC đáy CD có chiều cao bằng nhau và bằng 6cm, đáy AB = 2/3 CD => S ABC = 2/3 S DBC
Xét tiếp hai tam giác ABC và DBC đáy BC vì S ABC = 2/3 S DBC => AK = 2/3 DH
Xét tiếp tam giác AMC và tam giác DMC chung đáy MC mà chiều cao AK = 2/3 DH => SAMC = 2/3 S DMC
S DMC lớn hơn S AMC (12 . 6) / 2 = 36 cm²
S AMC = 36 / (3 – 2). 2 = 72 (cm²)
Xét tam giác AMC đáy AM, chiều cao CD => AM = 72 . 2 / 12 = 12 (cm)
Vậy độ dài cạnh AM là 12cm.
Bài tập 3
Mảnh đất hình thang có đáy lớn là 38m và đáy bé là 28m. Mở rộng hai đáy về bên phải của mảnh đất với đáy lớn thêm 9m và đáy bé thêm 8m thu được mảnh đất hình thang mới có diện tích lớn hơn diện tích mảnh đất hình thang ban đầu là 107,2 m². Hãy tính diện tích mảnh đất hình thang ban đầu.
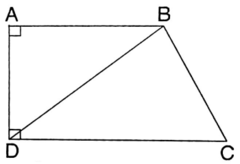
Lời giải:
Phần diện tích tăng thêm chính là diện tích của hình thang có đáy lớn bằng 9m và đáy bé là 8m, chiều cao bằng với chiều cao hình thang ban đầu.
Vậy chiều cao mảnh đất này sẽ là:
h = (107,1 x 2) / (9 + 8) = 12,6m
Diện tích mảnh đất hình thang ban đầu là:
S = [(38 + 28) / 2] x 12,6 = 415,8 (m²)
Vậy diện tích mảnh đất hình thang ban đầu là 415,8 m².
Qua bài viết trên, chúng ta đã biết được tính chất hình thang vuông và dấu hiệu để có thể nhận biết hình thang vuông. Mas.edu.vn hi vọng rằng các bạn đọc giả đã bổ sung thêm được một kiến thức Toán học thú vị nữa.
Tính chất hình thang vuông là một trong những khái niệm cơ bản trong hình học. Hình thang vuông được hình thành từ hai đường chéo có một góc vuông. Dưới đây là các tính chất quan trọng của hình thang vuông:
1. Hai đường chéo bằng nhau: Trong hình thang vuông, hai đường chéo có cùng độ dài. Điều này có nghĩa là độ dài từ một đỉnh đến đỉnh đối diện qua tâm đường tròn ngoại tiếp hình thang vuông là bằng nhau.
2. Tâm hình thang vuông: Hình thang vuông có một tâm đường tròn ngoại tiếp nằm trên đường chéo cắt nhau ở giao điểm của hai đường chéo. Tâm của hình thang vuông là điểm trung tâm của đường tròn ngoại tiếp và là điểm giao của hai đường chéo.
3. Tính chất góc: Trong hình thang vuông, ba đỉnh không nằm trên một đường thẳng. Góc tại một đỉnh của hình thang vuông bằng một nửa tổng hai góc vuông kề nhau tại đỉnh đó.
Bên cạnh đó, dưới đây là ba bài tập về hình thang vuông để áp dụng và củng cố kiến thức:
1. Cho một hình thang vuông ABCD với AB // CD, AB = 6cm và CD = 10cm. Tính độ dài đường chéo AC?
2. Trong một hình thang vuông ABCD, AC là đường chéo có độ dài 8cm. Gọi E là giao điểm của AB và CD. Tìm độ dài đoạn thẳng AE khi biết BE = 4cm.
3. Trong hình thang vuông ABCD, đường chéo AC cắt đường AB tạo thành góc xác định 75°. Tìm độ dài cạnh AD khi biết độ dài cạnh AB là 6cm.
Nhờ giải quyết những bài tập trên, ta có thể tổng hợp và vận dụng các tính chất của hình thang vuông, từ đó củng cố kiến thức và nắm vững khái niệm hình thang vuông.
Cảm ơn bạn đã xem bài viết Tính chất hình thang vuông? 3 bài tập về hình thang vuông tại Mas.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Hình thang vuông
2. Tính chất hình thang vuông
3. Đường cao hình thang vuông
4. Đường trung bình trong hình thang vuông
5. Chu vi hình thang vuông
6. Diện tích hình thang vuông
7. Công thức tính diện tích hình thang vuông
8. Công thức tính chu vi hình thang vuông
9. Tính chất các cạnh đối của hình thang vuông
10. Tính chất các góc trong hình thang vuông
11. Tính chất đối xứng của hình thang vuông
12. Tính chất tứ giác nội tiếp trong hình thang vuông
13. Tính chất tứ giác ngoại tiếp trong hình thang vuông
14. Tính chất tứ giác đồng dạng của hình thang vuông
15. Số đo các góc trong hình thang vuông.
Bài tập về hình thang vuông:
1. Tính diện tích hình thang vuông biết các cạnh a, b và chiều cao h.
2. Tính chu vi hình thang vuông biết các cạnh a, b và đường trung bình m.
3. Cho hình thang vuông ABCD có đáy AB = 6, đáy CD = 12 và đường cao h = 8. Tính diện tích và chu vi của hình thang vuông này.