Bạn đang xem bài viết Tính chất tam giác cân? 3 dạng bài tập thường gặp nhất tại Mas.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Tam giác cân là một trong những loại tam giác phổ biến và có nhiều tính chất độc đáo. Một tam giác được gọi là tam giác cân khi có hai cạnh bằng nhau và hai góc ở đỉnh tương ứng với hai cạnh bằng nhau cũng bằng nhau. Tính chất này không chỉ gây ấn tượng về mặt hình học mà còn có nhiều ứng dụng trong giải các bài toán toán học hay thực tế.
Đầu tiên, chúng ta có tính chất cơ bản của tam giác cân, đó là đối xứng qua đường trung trực của cạnh chung. Điều này có nghĩa là đường trung trực của cạnh chung của tam giác cân là đường trung trực cũng như đường đối xứng của tam giác.
Tiếp theo, tam giác cân có tính chất đặc biệt về trực tâm. Trực tâm của tam giác cân nằm trên 3 đỉnh cũng như đỉnh không chung của tam giác.
Cuối cùng, tam giác cân còn có khả năng chia làm hai tam giác đều bằng nhau khi vẽ đường cao từ đỉnh không chung. Điều này không chỉ giúp phân tích dễ dàng hơn mà còn có thể áp dụng để chứng minh các bài toán liên quan đến tam giác cân.
Ba dạng bài tập thường gặp nhất về tam giác cân bao gồm:
1. Chứng minh một tam giác là tam giác cân dựa trên các điều kiện cho sẵn.
2. Tính độ dài các cạnh và góc trong tam giác cân biết các điều kiện cho trước.
3. Giải các bài toán liên quan đến tam giác cân sử dụng tính chất của tam giác cân.
Với những tính chất đặc biệt này, tam giác cân không chỉ là một khái niệm hình học mà còn là một công cụ hữu ích trong việc giải quyết các bài toán toán học phức tạp.
Tam giác chính là loại hình có nhiều dạng nhất bao gồm tam giác cân, tam giác vuông,… Trong đó, tam giác cân chính là trọng tâm kiến thức ở môn toán hình lớp 7. Vậy tính chất tam giác cân là gì? Có những dạng bài tập nào liên quan đến tính chất tam giác cân? Hãy tìm hiểu cùng Mas.edu.vn nhé!
Danh Mục Bài Viết
Định nghĩa tam giác
Tam giác là gì?
Tam giác là loại hình cơ bản trong hình học. Tam giác là một hình hai chiều phẳng có ba đỉnh là ba điểm không thẳng hàng và ba cạnh là ba đoạn thẳng nối các đỉnh với nhau.
Tam giác là đa giác có số cạnh ít nhất. Và trong mọi trường hợp, tam giác luôn luôn là một đa giác đơn và luôn là một đa giác lồi.

Có những loại tam giác nào?
Trước khi tìm hiểu đến các tính chất tam giác cân, hãy cùng Mas.edu.vn xác định những loại của tam giác. Như đã đề cập trước đó, tam giác là hình gồm nhiều loại nhất, cụ thể như sau:
Tam giác thường
Tam giác thường là loại tam giác cơ bản nhất. Nó có độ dài ba cạnh khác nhau và các số đo góc trong cũng khác nhau.
Tam giác cân
Tam giác cân là tam giác có hai cạnh bằng nhau. Hai cạnh này được gọi là hai cạnh bên. Các tính chất của tam giác cân luôn được ứng dụng phổ biến trong các dạng bài tập. Những bài tập đó thường được đề cập nhiều trong đề thi.
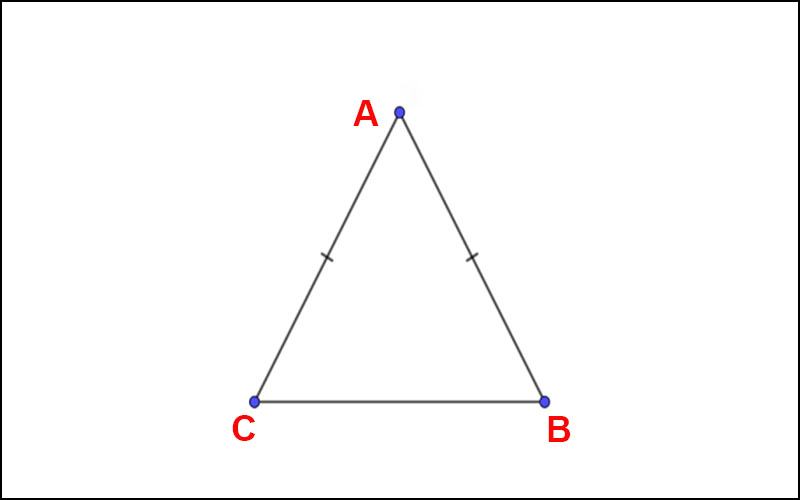
Tam giác đều
Tam giác đều là trường hợp đặc biệt của tam giác cân. Tam giác đều có cả ba cạnh và ba góc bằng nhau. Các tính chất của tam giác đều luôn bao gồm những tính chất của tam giác cân.
Tam giác cân
Định nghĩa tam giác cân là gì?
Tam giác cân là tam giác có hai góc ở đáy bằng nhau. Hoặc ngược lại, một tam giác có hai góc đáy bằng nhau thì đó là tam giác cân.
Một định nghĩa khác về tam giác cân nữa đó chính là khi một tam giác có hai cạnh bằng nhau thì đó là tam giác cân.
Dấu hiệu nhận biết tam giác cân
Các dấu hiệu nhận biết tam giác cân chính là những nội dung được đề cập trong phần định nghĩa nêu trên. Mas.edu.vn sẽ rút gọn những dấu hiệu nhận biết tam giác cân một cách dễ nhớ như sau:
- Tam giác có hai cạnh bằng nhau là tam giác cân.
- Tam giác có hai góc bằng nhau là tam giác cân.
Về phương diện kiến thức này có thể suy “xuôi” và đoán “ngược”. Từ những dấu hiệu bạn có thể nắm chắc được các tính chất tam giác cân và ngược lại.
Tính chất tam giác cân
Tính chất tam giác cân chính là phần trọng tâm của bài viết và cũng là điều các bạn cần ghi nhớ. Vì kiến thức này thường rất được sử dụng trong các đề thi cuối kỳ.
Các tính chất tam giác cân được liệt kê như sau:
- Trong một tam giác cân hai góc ở đáy bằng nhau.
- Nếu một tam giác có hai góc bằng nhau thì là tam giác cân.
- Hai cạnh của tam giác cân bằng nhau là a = a.
- Hai góc bằng nhau là góc b = góc b.
Hướng dẫn cách vẽ tam giác cân
Các tính chất tam giác cân vô cùng dễ nhớ và cách vẽ nó cũng không hề phức tạp. Dựa vào những tính chất tam giác cân, có hai cách đơn giản nhất để vẽ như sau:
Cách 1
- Bước 1: Vẽ 1 đoạn thẳng và chọn trung điểm của đoạn thẳng đó (đoạn thẳng này được xem là cạnh đáy của tam giác).
- Bước 2: Từ trung điểm đã xác định, vẽ đoạn thẳng vuông góc với đoạn thẳng ban đầu
- Bước 3: Nối hai điểm của đoạn thẳng đã cho với đỉnh đoạn thẳng vuông góc với cạnh đáy.
Cách 2
- Bước 1: Chấm một điểm bất kỳ.
- Bước 2: Vẽ hai đoạn thẳng bằng nhau có một điểm chung từ điểm đã cho.
- Bước 3: Nối hai điểm còn lại vào.
Kiến thức hữu ích:
- Tính chất trọng tâm tam giác và cách xác định trọng tâm
Tam giác vuông cân
Định nghĩa tam giác vuông cân là gì?
Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau. Tam giác vuông cân là một dạng đặc biệt khác từ tam giác cân.
Loại này thường được ứng dụng trong các dạng bài nâng cao vì các tính chất tam giác vuông cân của nó.
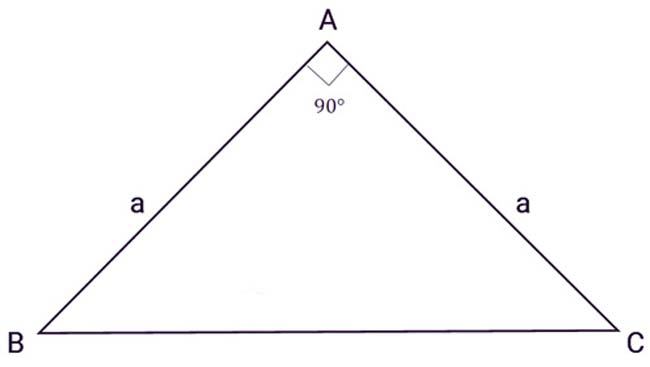
Tính chất tam giác vuông cân
Những tính chất tam giác vuông cân sẽ rộng hơn các tính chất tam giác cân. Cụ thể là:
- Tam giác vuông cân có hai góc ở đáy bằng nhau và bằng 45 độ.
- Trong tam giác vuông cân, các đường cao, đường trung tuyến, đường phân giác đều trùng nhau.
- Các đường đó đều có chiều dài bằng một nửa cạnh huyền.
Cách chứng minh tam giác vuông cân
Để chứng minh đâu là tam giác vuông cân thì ta sử dụng chính những tính chất của nó. Trong đó, phổ biến nhất là:
- Chứng minh một tam giác có 2 cạnh góc vuông bằng nhau.
- Chứng minh tam giác vuông có một góc 45 độ.
- Chứng minh tam giác cân có một góc đáy bằng 45 độ.
Một số công thức về tam giác cân
Công thức tính chu vi tam giác cân
Để tính chu vi tam giác cân, chúng ta cần biết đỉnh của tam giác cân và độ dài hai cạnh.
Từ đó, công thức tính chu vi hình tam giác cân là: P = 2a + c
- Trong đó, a là độ dài hai cạnh bằng nhau.
- c là độ dài cạnh còn lại.
Công thức tính diện tích tam giác cân
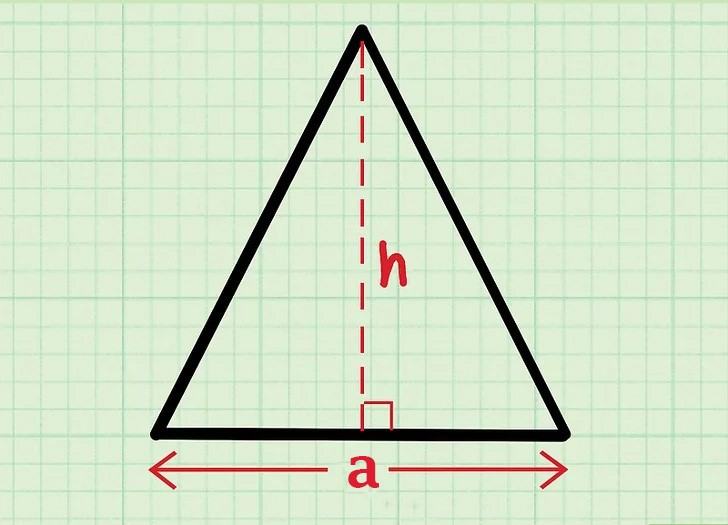
Để tính diện tích tam giác cân, chúng ta cần biết độ dài đường cao và cạnh đáy của tam giác cân.
Từ đó, công thức tính diện tích hình tam giác cân là: P = h*1/2 + a.
- Trong đó, h là độ dài đường cao của tam giác.
- a là cạnh đáy của tam giác cân.
Bài tập liên quan tới tam giác cân
Dạng 1: Bổ sung điều kiện sao cho hai tam giác cân bằng nhau
Cách giải: Dựa vào các trường hợp bằng nhau của hai tam giác và tính chất tam giác cân.
Ví dụ: Cho tam ABC cân tại A và tam giác A’B’C’. Cho biết cặp cạnh bên bằng nhau AB=A’B’. Hãy bổ sung thêm một điều kiện nữa để ( tam giác ABC = tam giác A’B’C)
Bài giải:
Để tam giác ABC = tam giác A’B’C’, ta cần bổ sung thêm một trong các điều kiện sau:
- Cặp cạnh đáy BC=B’C’, khi đó (tam giác ABC = tam giác A’B’C) (c.c.c)
- Cặp góc ở đỉnh bằng nhau (góc A = góc A’), khi đó (tam giác ABC = tam giác A’B’C) (c.g.c)
- Cặp góc ở đáy bằng nhau (góc B = góc B’), khi đó (tam giác ABC = tam giác A’B’C) (c.g.c hoặc g.c.g)
Dạng 2: Chứng minh hai đoạn thẳng bằng nhau nhờ định nghĩa tam giác cân
Cách giải: Dựa vào định nghĩa của tam giác cân
Ví dụ: Cho tam giác ABC cân tại A. Lấy các điểm D và E theo thứ tự thuộc các cạnh AB, AC sao cho AD = AE. Chứng minh rằng BE = CD.
Bài giải:
Ta có, tam giác ABC cân tại A thì
- AB=AC
- Góc A chung
- AD=AE (gt)
- Góc ABE = góc ACD
Suy ra BE=CD (đpcm)
Dạng 3: Sử dụng tính chất tam giác cân để tính góc hoặc chứng minh hai góc bằng nhau
Cách giải: Dựa vào tính chất tam giác cân
Ví dụ: Cho tam giác ABC cân tại A. Lấy điểm D thuộc cạnh AC, điểm E thuộc cạnh AB sao cho AD=AE
So sánh góc ABD và góc ACE.
Bài giải:
Do tam giác ABC cân tại A nên
- AB=AC
- Góc A chung
- AD=AE (gt)
Suy ra, tam giác ABD = tam giác ACE (c.g.c)
Từ đó, góc ABD = góc ACE (đpcm)
Tam giác IBC cân tại I.
Lưu ý khi làm bài tập về tam giác cân
Tính chất tam giác cân là phương pháp chủ yếu để giải những dạng bài về tam giác cân. Tuy nhiên, vẫn có một vài lưu ý khi làm những bài tập đó như sau:
- Vẽ hình vào nháp để xác định điều cần chứng minh.
- Đánh dấu đầy đủ những dữ kiện đề cho vào trong hình.
- Kẻ bảng giả thuyết và kết luận.
- Nên tìm ra nhiều cách cho một bài để linh hoạt khả năng giải toán.
- Quan trọng nhất, thuộc lòng những tính chất tam giác cân.
Nếu bạn nắm được các tính chất tam giác cân, vuông cân,… thì sẽ không có bài tập nào làm khó được bạn. Bài viết này đã thống kê đầy đủ các tính chất tam giác cân mà bạn cần biết. Đừng quên bổ sung kiến thức cùng Mas.edu.vn trong những bài viết sau nhé!
Tham khảo thêm:
- Tính chất của dãy tỷ số bằng nhau
- Tính chất đường trung trực của một đoạn thẳng? Top 10 bài tập vận dụng
Tính chất tam giác cân là một trong những khái niệm cơ bản trong hình học. Trên thực tế, tam giác cân xuất hiện rất phổ biến và có nhiều ứng dụng trong các bài toán và trường hợp thực tế.
Một tam giác cân là tam giác có hai cạnh bằng nhau. Điều này có nghĩa là hai góc ở đỉnh của tam giác cân cũng bằng nhau. Với tính chất này, chúng ta có thể suy ra một số tính chất quan trọng.
Đầu tiên, tính chất tam giác cân cho phép chúng ta dễ dàng tính góc của tam giác. Vì hai góc ở đỉnh của tam giác cân bằng nhau, ta chỉ cần chia đôi một góc ở đỉnh để tìm giá trị của góc kia. Việc này rất hữu ích khi phải tính toán các góc trong các bài toán hình học.
Thứ hai, tính chất tam giác cân còn giúp chúng ta xác định các đường cao và tâm đường tròn nội tiếp của tam giác. Một tam giác cân có đường cao đi qua đỉnh của tam giác và chia đôi cạnh đáy. Nhờ vậy, chỉ cần biết một cạnh và góc giữa hai cạnh, ta có thể tính toán chiều dài đường cao và diện tích của tam giác cân.
Cuối cùng, tính chất tam giác cân cho phép chúng ta giải quyết các bài toán về đồng dạng tam giác. Bằng cách sử dụng phép đồng dạng tam giác, ta có thể tìm các cạnh và các góc của một tam giác cân khi biết các thông tin về một tam giác cân khác. Điều này giúp tiết kiệm thời gian và dễ dàng áp dụng tính chất của tam giác cân trong các bài toán hình học phức tạp.
Tóm lại, tính chất tam giác cân là rất quan trọng và có ảnh hưởng lớn đến việc giải quyết các bài toán hình học. Hiểu về tính chất tam giác cân không chỉ giúp chúng ta rút ra các đặc điểm và tính chất của tam giác cân mà còn mở rộng cách suy nghĩ trong việc giải quyết các bài toán hình học khác.
Cảm ơn bạn đã xem bài viết Tính chất tam giác cân? 3 dạng bài tập thường gặp nhất tại Mas.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Tam giác cân
2. Đường trung tuyến tam giác cân
3. Đường cao tam giác cân
4. Đường phân giác trong tam giác cân
5. Đỉnh, đường bờ, góc nhọn tam giác cân
6. Trung điểm đáy triung tam tam giác cân
7. Tính chất các góc của tam giác cân
8. Phân tích các độ dài cạnh tam giác cân
9. Quan hệ giữa đáy tam giác cân và góc đối diện
10. Quan hệ giữa độ dài cạnh và đường cao tam giác cân
11. Công thức diện tích tam giác cân
12. Bài toán tìm đáy tam giác cân khi biết đường cao và diện tích
13. Bài toán tìm diện tích tam giác cân khi biết đáy và đường cao
14. Bài toán tìm đường cao tam giác cân khi biết đáy và diện tích
15. Bài toán tìm góc trong tam giác cân