Bạn đang xem bài viết Công thức tính đường cao trong tam giác đều dễ nhớ nhất tại Mas.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Đối với nhiều học sinh, việc tính toán trong môn toán thường được coi là một nhiệm vụ khó khăn và đòi hỏi tính nhớ cao. Tuy nhiên, trong một số trường hợp như tính đường cao trong tam giác đều, có thể áp dụng một công thức dễ nhớ để giải quyết vấn đề này.
Công thức tính đường cao trong tam giác đều được cho là dễ nhớ nhất bởi vì nó chỉ liên quan đến một giá trị duy nhất, đó chính là độ dài cạnh của tam giác đều đó. Theo đó, công thức đơn giản này có thể được viết dưới dạng:
“Đường cao trong tam giác đều bằng độ dài cạnh nhân căn ba.”
Việc sử dụng công thức này không chỉ giúp học sinh ghi nhớ dễ dàng mà còn giúp tăng tính sáng tạo và ứng dụng của họ trong việc giải quyết các bài toán liên quan đến tam giác đều. Bằng cách nhớ công thức một cách chính xác, học sinh có thể áp dụng nhanh chóng và chính xác trong việc tính toán độ dài đường cao của tam giác đều mà không cần phải dành nhiều thời gian suy nghĩ.
Như vậy, công thức tính đường cao trong tam giác đều dễ nhớ nhất là một công cụ hữu ích giúp giải quyết vấn đề tính toán trong môn toán. Việc nắm vững công thức này sẽ giúp học sinh tự tin hơn và nhanh chóng vượt qua các bài toán liên quan đến tam giác đều.
Bạn chưa biết cách tính đường cao trong tam giác đều? Đừng quá lo lắng, bài viết sau của Mas.edu.vn sẽ bật mí giúp bạn công thức tính đường cao trong tam giác đều. Mời bạn đọc tham khảo bài viết sau đây để biết rõ hơn.
Danh Mục Bài Viết
Đường cao trong tam giác đều là gì?
Tam giác đều là gì?
Trong hình học, tam giác đều được định nghĩa là tam giác có ba cạnh bằng nhau hoặc tương đương ba góc bằng nhau. Đồng thời mỗi góc bằng 60 độ. Tam giác đều hay còn gọi là đa giác đều với số cạnh bằng ba.
Sau khi biết khái niệm về tam giác đều, mời bạn đến nội dung tiếp theo của bài viết. Đó là đường cao trong tam giác đều là gì. Mời bạn đọc tham khảo nội dung sau để biết thêm chi tiết.
Đường cao trong tam giác đều là gì?
Đường cao trong tam giác đều là đoạn thẳng kẻ từ đỉnh của tam giác vuông góc với cạnh đáy. Độ dài của đường cao cũng chính là độ dài của đường thẳng đó.
Đường cao trong tam giác đều là đường trung trực chia cạnh đối diện thành hai phần bằng nhau. Đồng thời, đường cao trong tam giác đều cũng chính là đường phân giác ở đỉnh tam giác và đường trung tuyến.
Bên cạnh đó, đường cao của tam giác đều chia góc ở đỉnh thành hai góc có số đo bằng nhau. Ngoài ra, đường cao trong tam giác đều sẽ chia tam giác đó thành hai tam giác vuông bằng nhau.
Đường cao của một tam giác là đoạn vuông góc kẻ từ một đỉnh đến cạnh đối diện. Cạnh đối diện này được xem là đáy ứng với chiều cao. Độ dài của đường cao là khoảng cách từ đỉnh đến đáy. Mỗi tam giác gồm có 3 đường cao.
Vừa rồi là định nghĩa về đường cao trong tam giác đều. Tiếp nối bài viết là phần nội dung quan trọng, cách tính đường cao trong tam giác đều. Mời bạn đọc tham khảo nội dung sau cùng Mas.edu.vn.
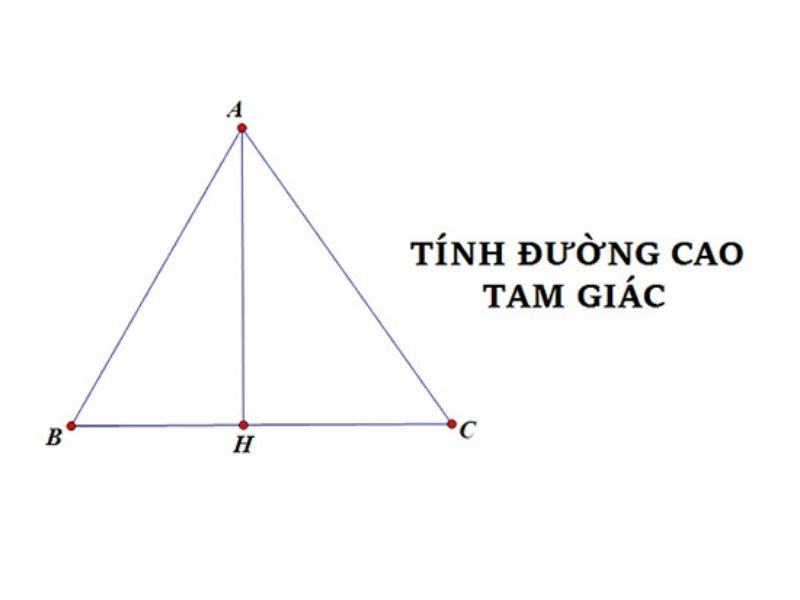
Cách tính đường cao trong tam giác đều
Tính đường cao trong tam giác đều dựa vào công thức Heron
Dưới đây là cách tính đường cao trong tam giác đều dựa vào công thức Heron. Mời bạn đọc cùng theo dõi để biết rõ hơn:
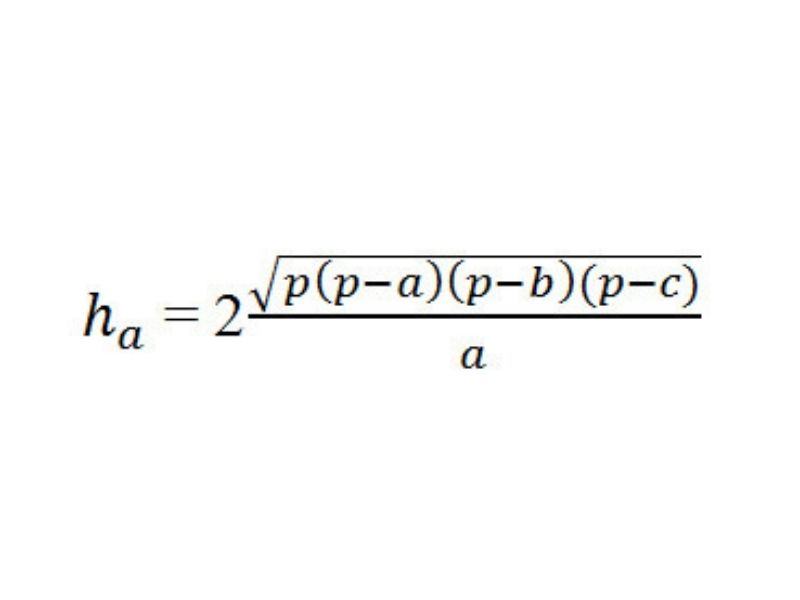
Trong đó:
- a, b, c: Lần lượt là độ dài các cạnh của tam giác.
- p: Nửa chu vi được tính theo công thức sau p = (a + b + c)/2.
- h: Chiều cao, ha là đường cao kẻ từ A xuống cạnh BC, hb là đường cao kẻ từ B xuống cạnh AC, hc là đường cao kẻ từ C xuống cạnh AB.
Thông tin trên của Mas.edu.vn đã bật mí giúp bạn cách tính đường cao tam giác đều dựa vào công thức Heron. Bạn nên ghi nhớ công thức này để vận dụng vào bài tập một cách dễ dàng. Mời bạn đọc tiếp tục theo dõi phần nội dung cuối cùng của bài viết.
Tính đường cao trong tam giác đều dựa vào công thức tính đường cao trong tam giác cân
Sau đây là công thức tính đường cao tam giác đều dựa vào công thức tính đường cao trong tam giác cân. Mời bạn đọc theo dõi bài viết của Mas.edu.vn để biết thêm chi tiết.
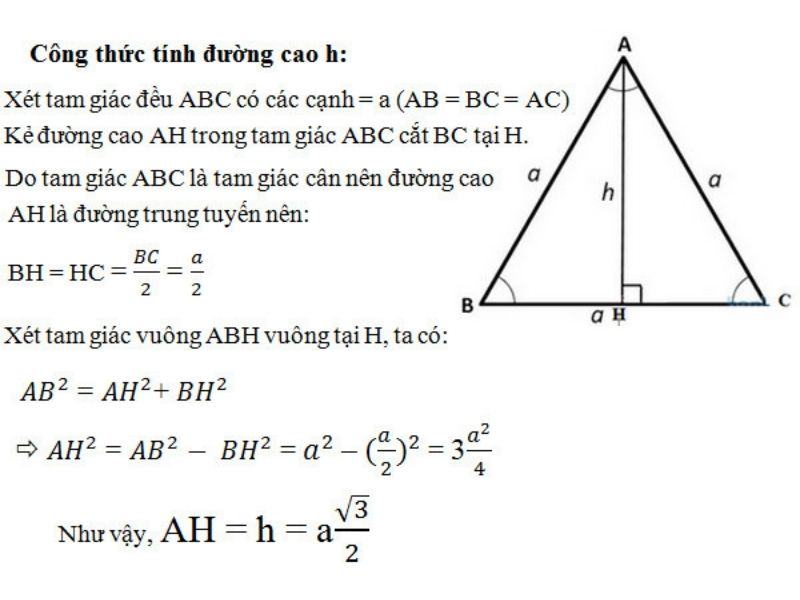
Xét tam giác đều ABC có các cạnh = a (AB = BC = AC). Kẻ đường cao AH trong trong tam giác ABC cắt BC tại H. Do tam giác ABC là tam giác cân nên đường cao AH là đường trung tuyến. Vì thế, chúng ta có công thức:
BH = HC = BC/2 = a/2.
Xét tam vuông ABH vuông tại H, ta có:
AB2 = AH2 + BH2
- AH2 = AB2 – BH2 = a2 – (a/2)2 = 3(a2/4)
- AH = h = a(/2)
Tam giác đều cũng là tam giác cân. Do đó, bạn có thể dựa vào đường cao của tam giác cân để tính đường cao của tam giác đều.
Xem thêm:
- Tính chất trọng tâm tam giác và cách xác định trọng tâm
- Tính chất ba đường cao của tam giác và bài tập áp dụng
Toàn bộ thông tin trên là những công thức về đường cao trong tam giác đều. Mong rằng bài viết của Mas.edu.vn sẽ giúp cho các bạn dễ hiểu và ghi nhớ cách tính đường cao tam giác đều. Đừng quên truy cập Mas.edu.vn thường xuyên để cập nhật những thông tin hay nhất nhé!
Trên thực tế, công thức tính đường cao trong tam giác đều là một trong những công thức cơ bản và quan trọng mà học sinh phải nắm vững trong môn toán học. Nhưng không phải lúc nào cũng dễ dàng để nhớ và áp dụng công thức này vào thực tế. Tuy nhiên, hãy tin rằng có một phương pháp dễ nhớ nhất cho công thức tính đường cao trong tam giác đều.
Chúng ta sẽ cùng nhìn vào bản thân tam giác đều để tìm hiểu cách dễ nhớ công thức này. Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau. Đặc điểm này tạo ra một cấu trúc hình học đơn giản và tương đối đều đặn.
Khi chúng ta chia tam giác đều thành hai tam giác vuông, ta sẽ có một tam giác vuông cân với một góc vuông và hai góc nhọn bằng nhau là 30 độ. Với độ dài cạnh của tam giác đều là a, ta có thể tính được độ dài đường cao của tam giác này.
Sử dụng tư duy hình học, ta có thể thấy rằng đường cao của tam giác đều là đường cao kẻ từ đỉnh vuông góc xuống đáy cạnh. Đồng thời, với tam giác vuông cân, ta biết rằng đường cao của tam giác nằm giữa hai đường trung tuyến và bằng một nửa độ dài cạnh đáy. Vậy công thức tính đường cao trong tam giác đều là:
đường cao = (cạnh đáy)/2 = a/2.
Chắc chắn rằng công thức trên rất dễ nhớ. Chỉ cần nhớ được rằng đường cao của tam giác đều bằng một nửa độ dài cạnh đáy, ta có thể tính đường cao mà không cần công thức hoặc công thức dễ nhớ tương tự.
Điều này giúp cho việc tính đường cao trong tam giác đều trở nên dễ dàng và thú vị hơn cho học sinh. Bằng cách kết hợp tư duy hình học và các công thức đơn giản, ta có thể nắm vững và ứng dụng công thức tính đường cao trong tam giác đều một cách linh hoạt và chính xác.
Trên thực tế, công thức tính đường cao trong tam giác đều dễ nhớ nhất là một cách tiếp cận sáng tạo và hiệu quả để giúp học sinh nắm bắt và ứng dụng kiến thức toán học một cách mượt mà. Việc tạo ra những phương pháp nhớ lâu và áp dụng linh hoạt là mục tiêu quan trọng trong giáo dục, và công thức tính đường cao trong tam giác đều không phải là ngoại lệ.
Cảm ơn bạn đã xem bài viết Công thức tính đường cao trong tam giác đều dễ nhớ nhất tại Mas.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Tam giác đều
2. Đường cao
3. Công thức tính
4. Tam giác cân
5. Tam giác vuông
6. Đường cao xuất phát từ đỉnh
7. Chiều cao
8. Cạnh tam giác
9. Đỉnh tam giác
10. Đoạn thẳng
11. Đường thẳng
12. Độ dài
13. Tính toán
14. Góc
15. Phép tính