Bạn đang xem bài viết Trực tâm là gì? 3 cách xác định trực tâm trong tam giác tại Mas.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Trực tâm – khái niệm quen thuộc trong hình học tam giác, đó là điểm đặc biệt trong tam giác mà qua đó có thể xác định được các đường trung tuyến, đường cao và đường phân giác. Trong bài viết này, chúng ta sẽ tìm hiểu về trực tâm và cách xác định nó qua ba phương pháp khác nhau. Mời các bạn cùng tìm hiểu!
Tính chất trực tâm trong tam giác là chủ đề quan trọng trong kiến thức Toán học. Nội dung chi tiết mời các bạn cùng Mas.edu.vn tham khảo bài viết trực tâm là gì?
Danh Mục Bài Viết
Trực tâm là gì?
Trực tâm là gì?
Nếu trong một tam giác, có ba đường cao giao nhau tại một điểm thì điểm đó được gọi là trực tâm.
Đường cao tam giác là đường vuông góc nối từ đỉnh tới cạnh đối diện của tam giác đó. Mỗi tam giác có 3 đường cao tương ứng với 3 đỉnh và cạnh đối diện.
Ví dụ: Tam giác ABC có ba đường cao là AM, BN, CP. Gọi H là giao điểm của ba đường cao trên thì H là trực tâm của tam giác ABC.
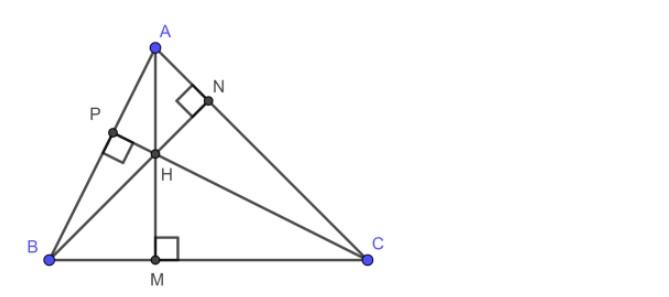
Tính chất trực tâm
Tính chất trực tâm trong tam giác là tài liệu rất hữu ích mà hôm nay Mas.edu.vn muốn giới thiệu đến các bạn lớp 7 tham khảo.
- Khoảng cách từ tâm đường tròn ngoại tiếp tam giác, đến trung điểm cạnh nối hai đỉnh còn lại bằng 1/2 khoảng cách từ một đỉnh tới trực tâm.
- Trực tâm tam giác vuông chính là đỉnh góc vuông của tam giác vuông đó.
- Trong tam giác cân thì đường cao cũng đồng thời là đường trung tuyến, đường phân giác và đường trung trực của đỉnh tam giác cân đó.
- Trong tam giác đều, trực tâm cũng đồng thời là trọng tâm, tâm đường tròn nội tiếp và ngoại tiếp của tam giác đó.
- Trực tâm nằm ở vùng phía trong 1 tam giác, nếu nó là tam giác nhọn.
- Trực tâm nằm ở vùng ngoài tam giác nếu nó là tam giác tù.
- Theo định lý Carnot: Đường cao tam giác ứng với một đỉnh cắt đường tròn ngoại tiếp tại điểm thứ hai là đối xứng của trực tâm qua cạnh tương ứng.
Sau khi hiểu rõ về trực tâm là gì và tính chất của nó thì cùng Mas.edu.vn đến cách xác định trực tâm trong 3 loại tam giác nhé!
Hướng dẫn cách xác định trực tâm
Đối với mỗi loại tam giác sẽ có vị trí và cách xác định trực tâm khác nhau:
Trực tâm trong tam giác nhọn
Đầu tiên, cùng Mas.edu.vn điểm qua trực tâm là gì trong tam giác nhọn ngay nhé!
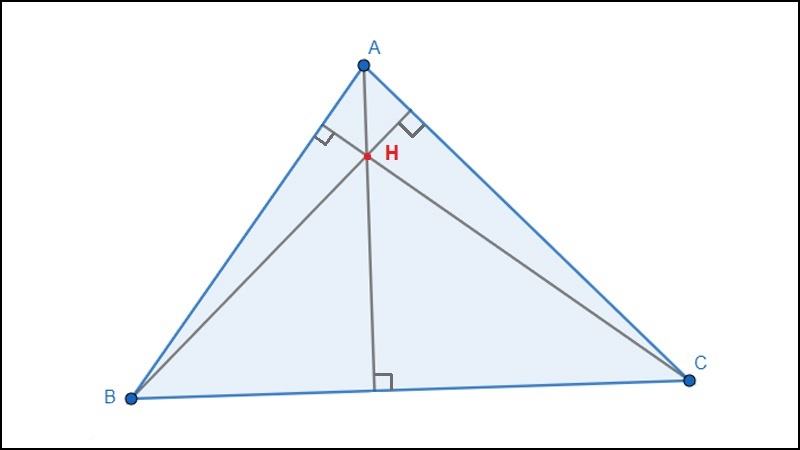
Trực tâm nằm ở miền trong tam giác nhọn.
Ví dụ: Tam giác nhọn ABC có trực tâm H nằm ở miền trong tam giác.
Trực tâm trong tam giác vuông
Tiếp theo, cùng Mas.edu.vn điểm qua trực tâm là gì trong tam giác vuông có gì khác biệt ngay nhé!
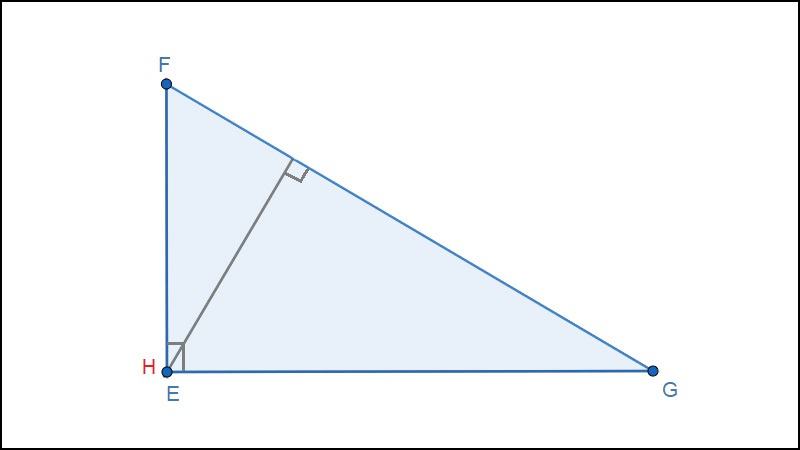
Trực tâm trong tam giác vuông chính là đỉnh góc vuông.
Ví dụ: Tam giác vuông EFG có trực tâm H trùng với góc vuông E.
Trực tâm trong tam giác tù
Cuối cùng, trực tâm là gì trong tam giác tù có gì đặc biệt, tìm hiểu thôi nào!
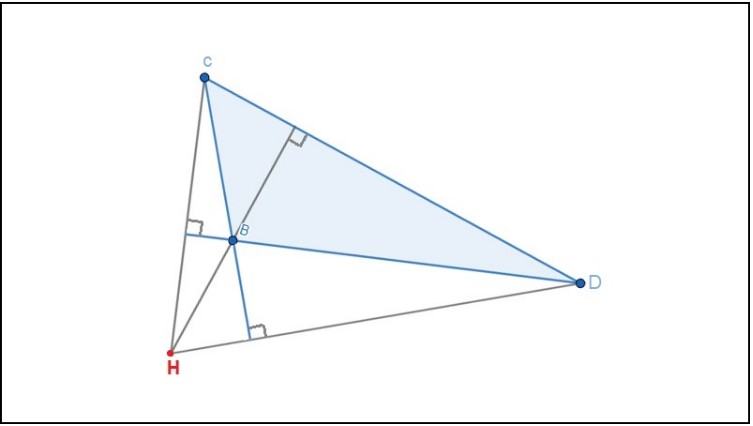
Trực tâm trong tam giác tù là nằm ở miền ngoài tam giác đó.
Ví dụ: Tam giác tù BCD có trực tâm H nằm ở miền ngoài tam giác.
Bài tập liên quan đến trực tâm
Qua những câu hỏi trên chắc hẳn bạn đã hiểu rõ các khái niệm và tính chất trực tâm là gì trong tam giác. Vậy cùng Mas.edu.vn củng cố kiến thức qua một số bài tập liên quan đến trực tâm là gì nhé!
Bài 1: Cho tam giác ABC không vuông. Gọi H là trực tâm của nó. Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ra trực tâm của tam giác đó.
Hướng dẫn giải:
Gọi D, E, F là chân các đường vuông góc kẻ từ A, B, C của ΔABC.
⇒ AD ⟘ BC, BE ⟘ AC, CF ⟘ AB.
ΔHBC có :
- AD ⊥ BC nên AD là đường cao từ H đến BC.
- BA ⊥ HC tại F nên BA là đường cao từ B đến HC.
- CA ⊥ BH tại E nên CA là đường cao từ C đến HB.
Mà AD, BA, CA cắt nhau tại A nên A là trực tâm của ΔHCB.
Bài 23 trang 65 Hình học 10 Nâng cao
Gọi H là trực tâm của tam giác không vuông ABC. Chứng minh rằng bán kính các đường tròn ngoại tiếp các tam giác ABC, HBC, HCA, HAB bằng nhau.
Hướng dẫn giải:
Trường hợp 1: Tam giác ABC có ba góc nhọn.
Gọi R, R1 lần lượt là bán kính đường tròn ngoại tiếp tam giác ABC, HBC.
Áp dụng định lí sin ta có:
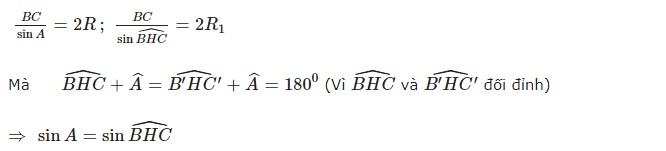
Do đó 2R=2R1 ⇒ R=R1.
Vậy bán kính đường tròn ngoại tiếp tam giác HBC bằng bán kính đường tròn ngoại tiếp tam giác ABC.
Tương tự bán kính đường tròn ngoại tiếp tam giác HCA,HAB bằng bán kính đường tròn ngoại tiếp tam giác ABC.
Trường hợp 2: Tam giác ABC có góc tù.
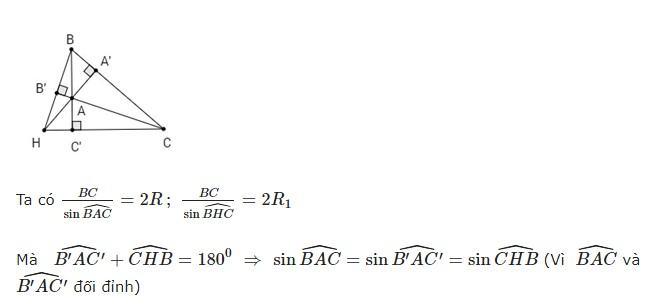
⇒ R = R1
Tương tự ta chứng minh được bán kính đường tròn ngoại tiếp tam giác HCA,HAB bằng bán kính đường tròn ngoại tiếp tam giác ABC.
Câu 70 trang 50 Sách Bài Tập Toán lớp 7 tập 2
Cho tam giác ABC vuông tại B. Điểm nào là trực tâm của tam giác đó?
Hướng dẫn giải:
∆ABC vuông tại B => AB⊥BC nên AB là đường cao từ đỉnh A.
⇒CB⊥AB nên CB là đường cao kẻ từ đỉnh C.
B là giao điểm của 2 đường cao AB và CB. Vậy B là trực tâm của ∆ABC.
Câu 71 trang 50 Sách Bài Tập Toán lớp 7 tập 2
a) Chứng minh rằng: CI⊥AB.
b) Cho ˆACB=40. Tính ˆBID,ˆDIE
Hướng dẫn giải:
a) Trong ∆ABC ta có hai đường cao AD và BE cắt nhau tại I nên I là trực tâm của ∆ABC
⇒⇒ CI là đường cao thứ ba
Vậy CI⊥ABCI⊥AB
b) Áp dụng trực tâm là gì trong tam giác vuông BEC có:
ˆBEC=90∘
⇒ˆEBC+ˆC=90∘ (tính chất tam giác vuông)
⇒ˆEBC=90∘−ˆC=90∘−40∘=50∘ hay ˆIBD=50∘
Trong tam giác IDB có ˆIDB=90∘
⇒ˆIBD+ˆBID=90∘ (tính chất tam giác vuông)
BID^=90∘−IBD^=90∘−50∘=40∘
BID^+DIE^=180∘ (2 góc kề bù)
⇒ˆDIE=180∘−ˆBID=180∘−40∘=140∘

Bài viết trên đã tóm tắt khái niệm trực tâm là gì trong tam giác và một số tính chất của nó. Hy vọng với những kiến thức tổng hợp trên sẽ hữu ích với độc giả. Nếu thấy hay nhớ like và chia sẻ giúp Mas.edu.vn nhé!
Kết Luận:
Trực tâm là một khái niệm quan trọng trong hình học tam giác, nó được xác định như là giao điểm của ba đường trung tuyến của tam giác. Trực tâm cũng được gọi là trọng tâm của tam giác, vì nó chia tam giác thành ba phần có diện tích bằng nhau.
Có ba cách xác định trực tâm trong tam giác. Cách đầu tiên là sử dụng công thức tính toán, cách này phức tạp và khá rườm rà. Cách thứ hai là sử dụng đường trung tuyến, chúng ta có thể tìm trực tâm bằng cách vẽ ba đường trung tuyến của tam giác và tìm giao điểm của chúng. Cách thứ ba là sử dụng tính chất của trực tâm, nếu ta có được một điểm nằm trên một đỉnh của tam giác và trực tâm, thì ta có thể kéo dúi hình vuông từ đỉnh đó đến trực tâm và nối thẳng hai đỉnh còn lại. Giao điểm của hai đường thẳng này chính là trực tâm của tam giác.
Trực tâm có vai trò quan trọng trong hình học tam giác. Nó là trọng tâm của tam giác, nên có thể giúp chúng ta tính toán và xác định một số thuộc tính của tam giác một cách dễ dàng. Trực tâm cũng có tác dụng cân bằng tam giác, khiến các tác động lực tác động lên tam giác trở nên đồng đều và ổn định hơn.
Cảm ơn bạn đã xem bài viết Trực tâm là gì? 3 cách xác định trực tâm trong tam giác tại Mas.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Trực tâm: điểm giao của ba đường trung tuyến trong tam giác.
2. Tam giác trực tâm: tam giác mà trực tâm của nó trùng với trọng tâm.
3. Đỉnh trực tâm: điểm giao của các trung trực của các đỉnh của tam giác.